Before we proceed with more examples, we need to add another thermodynamic tool. Unfortunately, there are no “internal energy” or “enthalpy” meters. In fact, these state properties must be “measured” indirectly by other state properties. The Gibbs phase rule tells us that if two state variables are fixed in a pure single-phase system, then all other state variables will be fixed. Therefore, it makes sense to measure these properties in terms of P, V, and T. In addition, if this relation is developed, it will enable us to find P, V, and/or T changes for a given change in ΔU or ΔH. In Example 2.3, where a warm and cold steel blocks were contacted, we solved the problem without calculating the change in temperature for each block. However, if we had a relation between U and T, we could have calculated the temperature changes. The relations that we seek are the definitions of the heat capacities.
Constant Volume Heat Capacity
The constant of proportionality between the internal energy change at constant volume and the temperature change is known as the constant volume heat capacity. The constant volume heat capacity is defined by:
Since temperature changes are easily measured, internal energy changes can be calculated once CV is known. CV is not commonly tabulated, but, as shown below, it can be easily determined from the constant pressure heat capacity, which is commonly available.
Constant Pressure Heat Capacity
In the last two sections, we have introduced enthalpy, and we can relate the change in enthalpy of a system to temperature in a manner analogous to the method used for internal energy. This relationship will involve a new heat capacity, the heat capacity at constant pressure defined by:
where H is the enthalpy of the system.
The use of two heat capacities, CV and CP, forces us to think of constant volume or constant pressure as the important distinction between these two quantities. The important quantities are really internal energy versus enthalpy. You simply must convince yourself to remember that CV refers to changes in U at constant volume, and CP refers to changes in H at constant pressure.
Relations between Heat Capacities, U and H
We have said that CV values are not readily available; therefore, how do we determine internal energy changes? Also, how do we determine enthalpy changes at constant volume or internal energy changes at constant pressure? We will return to the details of these questions in Chapters 6–8 and handle them rigorously, but the details have been rigorously followed by developers of thermodynamic charts and tables. Therefore, for relating the internal energy or enthalpy to temperature and pressure, a thermodynamic chart or table is preferred. If none is available, or properties are not tabulated in the state of interest, some exact relations and some approximate rules of thumb must be applied. The relations are also useful for introductory calculations while focus is on the energy balance rather than the property relations.
For an ideal gas,
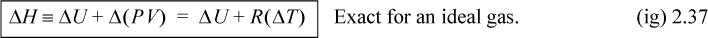
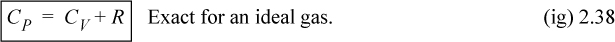
CP, CV and relation between ΔU and ΔH for an ideal gas.
Constant pressure heat capacities for ideal gases are tabulated in Appendix E. Constant volume heat capacities for ideal gases can readily be determined from Eqn. 2.38. For ideal gases, internal energy and enthalpy are independent of pressure as we implied with Eqn. 1.21. For real gases and for liquids, the relation between CP and CV is more complex, and derivatives of P-V-T properties must be used as shown rigorously in Examples 6.1, 6.6, and 6.9 and implemented thereafter. We will use thermodynamic tables and charts for real gases until these relations are developed.
For liquids or solids, we typically calculate ΔH and correct the calculation if necessary as explained below. For liquids, it has been experimentally determined that internal energy is only very weakly dependent on pressure below Tr = 0.75. In addition, the molar volume is insensitive to pressure below Tr = 0.75. We demonstrated in Example 2.4 that,
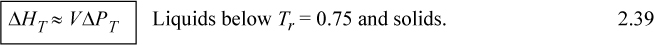
Pressure dependence of H for condensed phases.
is the reduced temperature calculated by dividing the absolute temperature by the critical temperature. (A rigorous evaluation is considered in Example 6.1 on page 233.) The relations for solids and liquids are important because frequently the properties have not been measured, or the measurements available in charts and tables are not available at the pressures of interest. We may then summarize the relations of internal energy and enthalpy with temperature.
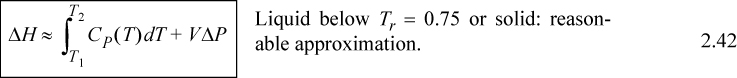
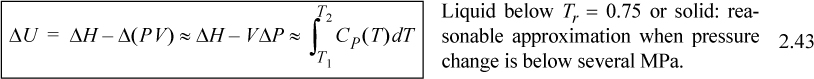
Useful formula for relating T, P to U and H in the absence of phase changes.
Note: These formulas do not account for phase changes which may occur.
Note that the heat capacity of a monatomic ideal gas can be obtained by differentiating the internal energy as given in Chapter 1, resulting in CV = 3/2 R and CP = 5/2 R. Heat capacities for diatomics are larger, CP = 7/2 R, and CV = 5/2 R near room temperature, and polyatomics are larger still. According to classical theory, each degree of freedom5 contributes 1/2R to CV. Kinetic and potential energy each contribute a degree of freedom in each dimension. A monatomic ideal gas has only three kinetic energy degrees of freedom, thus CV = 3/2 R. Diatomic molecules are linear so they have two additional degrees of freedom for the linear (one-dimensional) bond that has kinetic and potential energy both. In complicated molecules, the vibrations are characterized by modes. See the endflap to make a quick comparison. Monatomic solids have three degrees of freedom each for kinetic and vibrational energy, one for each principle direction, thus the law of Dulong and Petit, CVS = 3R is a first approximation. Low-temperature heat capacities of monatomic solids are explored more in Example 6.8. If you become curious about the manner in which the heat capacities of polyatomic species differ from those of the spherical molecules discussed in Chapter 1, you will find introductions to statistical thermodynamics explain the contributions of translation, rotation, and vibration. For polyatomic molecules, the heat capacity increases with molecular weight due to the increased number of degrees of freedom for each bond. In this text, ideal gas heat capacity values at 298 K are summarized inside the back cover of the book, and may be assumed to be independent of temperature over small temperature ranges near room temperature. The increase in heat capacity with temperature for diatomics and polyatomics is dominated by the vibrational contribution. The treatment of heat capacity by statistical thermodynamics is particularly interesting because it is a theory6 that often gives more accurate results than experimental calorimetric measurements. Commonly, engineers correlate ideal gas heat capacities with expressions like polynomials.
Whenever we assume heat capacity to be temperature independent in this text, we mark the equation with a (*) symbol near the right margin.
We will frequently ignore the heat capacity dependence on T to make an approximate calculation. Whenever we assume heat capacity to be temperature independent in this text, we mark the equation with a (*) symbol near the right margin. Heat capacities represented as polynomials of temperature are available in Appendix E. The heat capacity depends on the state of aggregation. For example, water has a different heat capacity when solid (ice), liquid, or vapor (steam). The contribution of the heat capacity integral to the energy balance is frequently termed the sensible heat to communicate its contribution relative to latent heat (due to phase changes) or heat of reaction to be discussed later. Note that these are called “heats” even though they are enthalpy changes.
The heat capacity of a substance depends on the state of aggregation.
Example 2.5. Enthalpy change of an ideal gas: Integrating CPig(T)
Propane gas undergoes a change of state from an initial condition of 5 bar and 105°C to 25 bar and 190°C. Compute the change in enthalpy using the ideal gas law.
Solution
The ideal gas change is calculated via Eqn. 2.41 and is independent of pressure. The heat capacity constants are obtained from Appendix E.
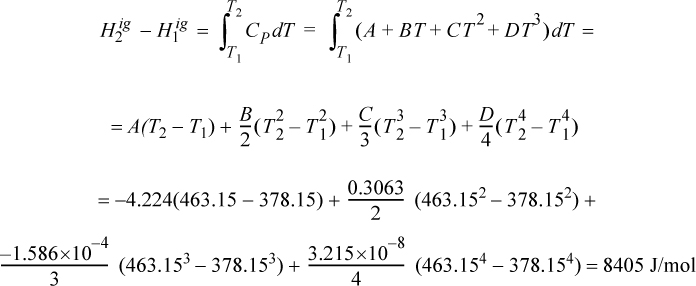
Example 2.6. Enthalpy of compressed liquid
The compressed liquid tables are awkward to use for compressed liquid enthalpies because the pressure intervals are large. Using saturated liquid enthalpy values for water and hand calculations, estimate the enthalpy of liquid water at 20°C H2O and 5 and 50 MPa. Compare to the values obtained using the compressed liquid steam tables.
Solution
This is a common calculation needed for working with power plant condensate streams at high pressure. The relevant equation is Eqn. 2.42, but we can eliminate the temperature integral by selecting saturated water at the same temperature and then applying the pressure correction, i.e., applying Eqn. 2.39, ΔH ≈ VΔP relative to the saturation condition, giving H = Hsat + VΔP. The numerical calculations have already been done in Example 2.4 on page 55. Both calculations use the same approximation, even though the paths are slightly different. A more rigorous analysis is shown later in Example 6.1.
This is a common calculation needed for working with power plant condensate streams at high pressure.
Example 2.7. Adiabatic compression of an ideal gas in a piston/cylinder
Nitrogen is contained in a cylinder and is compressed adiabatically. The temperature rises from 25°C to 225°C. How much work is performed? Assume that the heat capacity is constant (CP/R = 7/2), and that nitrogen follows the ideal gas law.
Solution
System is the gas. Closed system, system size changes, adiabatic.
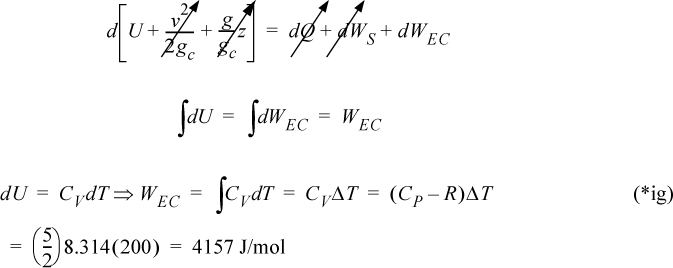
Note that because the temperature rise is specified, we do not need to know if the process was reversible.
Relation to Property Tables/Charts
In Section 1.4, we used steam tables to find internal energies of water as liquid or vapor. Tables or charts usually contain enthalpy and internal energy information, which means that these properties can be read from the source for these compounds, eliminating the need to apply Eqns. 2.40–2.43. This is usually more accurate because the pressure dependence of the properties that Eqns. 2.40–2.43 neglect has been included in the table/chart, although the pressure correction method applied in the previous example for liquids is generally accurate enough for liquids. Energy and enthalpy changes spanning phase transitions can be determined directly from the tables since energies and enthalpies of phase transitions are implicitly included in tabulated values.
Estimation of Heat Capacities
If heat capacity information cannot be located from appendices in this text, from the NIST Chemistry WebBook7, or from reference handbooks, it can be estimated by several techniques offered in the Chemical Engineer’s Handbook8 and The Properties of Gases and Liquids.9
Phase Transitions (Liquid-Vapor)
Enthalpies of vaporization are tabulated in Appendix E for selected substances at their normal boiling temperatures (their saturation temperatures at 1.01325 bar). In the case of the steam tables, Section 1.4 shows that the energies and enthalpies of vaporization of water are available along the entire saturation curve. Complete property tables for some other compounds are available in the literature or online, however, most textbooks present charts to conserve space, and we follow that trend. In the cases where tables or charts are available, their use is preferred for phase transitions away from the normal boiling point, although a hypothetical path that passes through the normal boiling point can usually be constructed easily.
The energy of vaporization is more difficult to find than the enthalpy of vaporization. It can be calculated from the enthalpy of vaporization and the P-V-T properties. Since U = H – PV,
ΔUvap = ΔHvap – Δ(PV)vap = ΔHvap – (PsatV)V – (PsatV)L = ΔHvap – Psat(VV – VL)
Far from the critical point, the molar volume of the vapor is much larger than the molar volume of the liquid. Further, at the normal boiling point (the saturation temperature at 1.01325 bar), the ideal gas law is often a good approximation for the vapor volume,
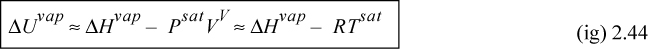
Relation between ΔUvap and ΔHvap when the vapor follows the ideal gas law.
Estimation of Enthalpies of Vaporization
If the enthalpy of vaporization cannot be located in the appendices or a standard reference book, it may be estimated by several techniques offered and reviewed in the Chemical Engineer’s Handbook and The Properties of Gases and Liquids. One particularly convenient correlation is10
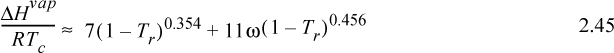
Generalized correlation for ΔHvap.
where Tr is reduced temperature, ω is the acentric factor (to be described in Chapter 7), also available on the back flap. If accurate vapor pressures are available, the enthalpy of vaporization can be estimated far from the critical point (i.e., Tr < 0.75) by the Clausius–Clapeyron equation:
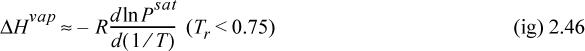
The background for this equation is developed in Section 9.2. Vapor pressure is often represented by the Antoine equation, logPsat = A – B/(T + C). If Antoine parameters are available, they may be used to estimate the derivative term of Eqn. 2.46,
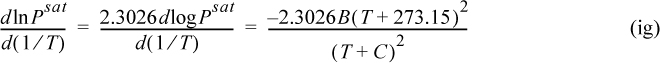
where T is in °C, and B and C are Antoine parameters for the common logarithm of pressure. For Antoine parameters intended for other temperature or pressure units, the equation must be carefully converted. The temperature limits for the Antoine parameters must be carefully followed because the Antoine equation does not extrapolate well outside the temperature range where the constants have been fit. If Antoine parameters are unavailable, they can be estimated to roughly 10% accuracy by the shortcut vapor pressure (SCVP) model, discussed in Section 9.3,
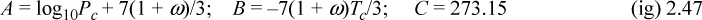
where the units of Pc match the units of Psat, Tc is in K, and T is in °C.
Phase Transitions (Solid-Liquid)
Enthalpies of fusion (melting) are tabulated for many substances at the normal melting temperatures in the appendices as well as handbooks. Internal energies of fusion are not usually available, however the volume change on melting is usually very small, resulting in internal energy changes that are nearly equal to the enthalpy changes:
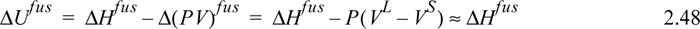
Unlike the liquid-vapor transitions, where Tsat depends on pressure, the melting (solid-liquid) transition temperature is almost independent of pressure, as illustrated schematically in Fig. 1.7.
Leave a Reply