Integral Equations

The differential equations representing the behavior of the system are obtained by the application of conservation principles to a differential element. Integration of these differential equations leads to expressions that describe the overall behavior of the entire system. Many of the differential equations can be integrated analytically, yielding algebraic or transcendental equations. However, such analytical integration is not always possible, and numerical computation is necessary for obtaining the integrals [4]. The determination of reactor volume often involves equations of the following form [6]:

Here, F_A0 is the molar flow rate of species A, and −r_A is the rate of reaction, which is a function of conversion X_A. Equation 4.13 is represented by Figure 4.6, where the shaded region represents the integral and is equal to the quantity V/F_A0.

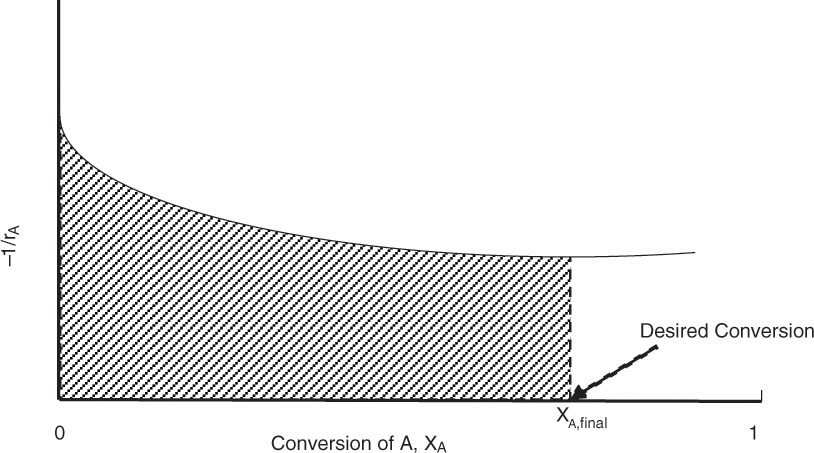
Figure 4.6 Determination of reactor volume.

When the reaction rate cannot be easily integrated analytically, the shaded region—the area under the curve—is evaluated numerically.