There is one implication of non-ideal fluid behavior that should be clear from the equations presented above: Real fluids behave differently from ideal gases. How differently? An example provides the most straightforward answer to that question. Here we adapt some of the derivatives from Chapter 6.
Example 7.6. Derivatives of the Peng-Robinson equation
Determine 
, 
, and 
for the Peng-Robinson equation.
Solution
The derivatives (∂U/∂V)T and (∂CV/∂V)T have been written in terms of measurable properties in Examples 6.6 and 6.9, respectively, and have been evaluated for an ideal gas. The analysis with the Peng-Robinson model provides more realistic representation of the properties of real substances. Beginning with the same analytical expressions set forth in the referenced examples, a key derivative is obtained for the Peng-Robinson equation,
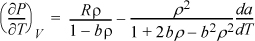
which approaches the ideal gas limit: 
. The volume dependence of CV is obtained by the second derivative:
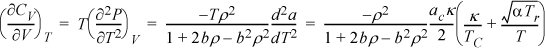
which approaches the ideal gas limit of zero at low density,
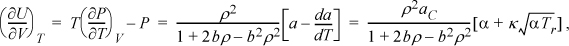
which also approaches the ideal gas limit of zero at low density. We have thus shown that CV depends on volume. To calculate a value of CV, first we determine 
, where 
is the heat capacity tabulated in Appendix E. Then, at a given {P,T}, the equation of state is solved for ρ. The resultant density is used as the limit in the following integrals, noting as V → ∞, ρ → 0, and dV = –dρ/ρ2: This method is used for departures from ideal gas properties in Chapter 8.
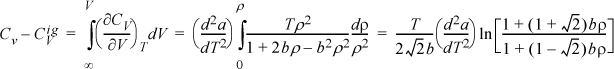
where 
Leave a Reply