In this section we introduce the Carnot cycle as a method to convert heat to work. Many power plants work on the same general principle of using heat to produce work. In a power plant, heat is generated by coal, natural gas, or nuclear energy. However, only a portion of this energy can be used to generate electricity, and the Carnot cycle analysis will be helpful in understanding those limitations. Before we start the analysis, let us define the ratio of net work produced to the heat input as the thermal efficiency using the symbol ηθ:
We wish to make the thermal efficiency as large as possible. We prove in the next chapter that the Carnot engine matches the highest thermal efficiency for an engine operating between two isothermal reservoirs. Maximizing thermal efficiency is a design goal that pervades Units I and II. We reconsider the thermal efficiency each time we add a layer of sophistication in our analysis. The concept of entropy in Chapter 4 will help us to generalize from ideal gases to steam or other fluids with available tables and charts. The calculus of classical thermodynamics in Chapter 5 will help to generalize to any substance, making our own tables and charts in Chapters 6–9. Evaluating the thermal efficiency in many situations is a skill that any engineer should have. Chemical engineering embraces a broad scope of … “chemicals.”
The Carnot Engine
The Carnot cycle was conceived by Sadi Carnot as a route to convert heat into work. In the previous chapter, we developed the energy balances and work calculations for reversible isothermal and adiabatic processes. The Carnot engine combines them in a cycle. Consider a piston in the vicinity of both a hot reservoir and a cold reservoir as illustrated in Fig. 3.1. The insulation on the piston may be removed to transfer heat from the hot reservoir during one step of the process, and also removed from the cold side to transfer heat to the cold reservoir during another step of the process. Carnot conceived of the cycle consisting of the steps shown schematically on the P-V diagram beginning from point a. Between points a and b, the gas undergoes an isothermal expansion, absorbing heat from the hot reservoir. From point b to c, the gas undergoes an adiabatic expansion. From point c to d, the gas undergoes an isothermal compression, rejecting heat to the cold reservoir. From point d to a, the gas undergoes an adiabatic compression to return to the initial state.
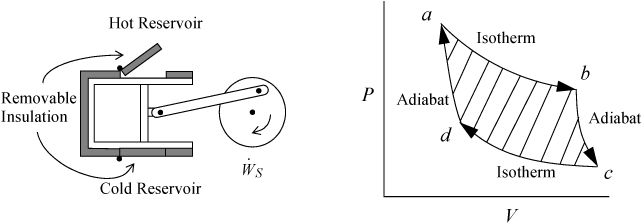
Figure 3.1. Schematic of the Carnot engine, and the Carnot P-V cycle when using a gas as the process fluid.
The Carnot cycle is one method of constructing a heat engine.
Nicolas Léonard Sadi Carnot (1796–1832) was a French scientist who developed the Carnot cycle to demonstrate the maximum conversion of heat into work.
Let us consider the energy balance for the gas in the piston. Because the process is cyclic and returns to the initial state, the overall change in U is zero. The system is closed, so no flow work is involved. This work performed, WEC = ∫PdV for the gas, is equal to the work done on the shaft plus the expansion/contraction work done on the atmosphere for each step. By summing the work terms for the entire cycle, the net work done on the atmosphere in a complete cycle is zero since the net atmosphere volume change is zero. Therefore, the work represented by the shaded portion of the P-V diagram is the useful work transferred to the shaft.
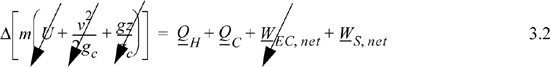
You can see from the shaded area in Fig. 3.1 that –WS, net > 0; therefore, since QH > 0 and QC < 0, 
. The ratio 
is negative, and to maximize η we seek to make QC as small in magnitude as possible.
The heat transferred and work performed in the various steps of the process are summarized in Table 3.1. For this calculation we assume the gas within the piston follows the ideal gas law with temperature-independent heat capacities. We calculate reversible changes in the system; thus, we neglect temperature and velocity gradients within the gas (or we perform the process very slowly so that these gradients do not develop).
Table 3.1. Illustration of Carnot Cycle Calculations for an Ideal Gas.a
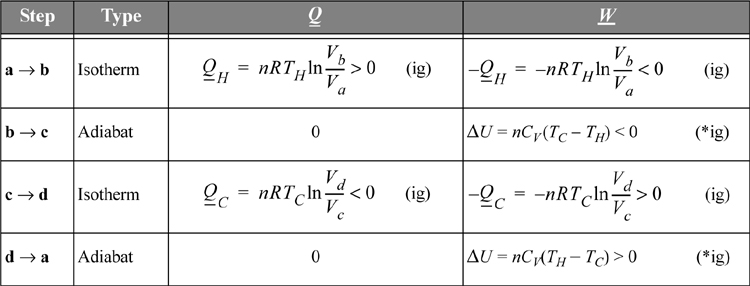
a. The Carnot cycle calculations are shown here for an ideal gas. There are no requirements that the working fluid is an ideal gas, but it simplifies the calculations.
Note: The temperatures TH and TC here refer to the hot and cold temperatures of the gas, which are not required to be equal to the temperatures of the reservoirs for the Carnot engine to be reversible. In Chapter 4 we will show that if these temperatures do equal the reservoir temperatures, the work is maximized.
Comparing adiabats b → c and d → a, the work terms must be equal and opposite since the temperature changes are opposite. The temperature change in an adiabatic process is related to the volume change in Eqn. 2.63. In that equation, when the temperature ratio is inverted, the volume ratio is inverted. Therefore, we reason that for the two adiabatic steps, Vb/Va = Vc/Vd. Using the ratio in the formulas for the isothermal steps, the ratio of heat flows becomes
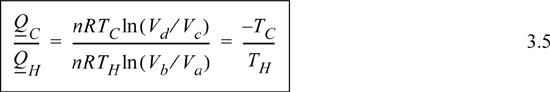
Inserting the ratio of heat flows into Eqn. 3.4 results in the thermal efficiency.
The thermal efficiency of a heat engine is determined by the upper and lower operating temperatures of the engine.
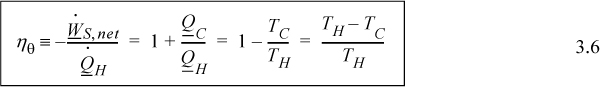
You must use absolute temperature when applying Eqn. 3.6. We can skip the conversion to absolute temperature in the numerator of the last term because the subtraction means that the 273.15 (for units of K) in one term is canceled by the other. There is no such cancellation in the denominator.
Eqn. 3.6 indicates that we cannot achieve ηθ = 1 unless the temperature of the hot reservoir becomes infinite or the temperature of the cold reservoir approaches 0 K. Such reservoir temperatures are not practical for real applications. For real processes, we typically operate between the temperature of a furnace and the temperature of cooling water. For a typical power-plant cycle based on steam as the working fluid, these temperatures might be 900 K for the hot reservoir and 300 K for the cold reservoir, so the maximum thermal efficiency for the process is near 67%, theoretically. Most real power plants operate with thermal efficiencies closer to 30% to 40% owing to inherent inefficiencies in real processes.
Perspective on the Heat Engine
The Carnot cycle provides a quick and convenient guideline for processes that seek to convert heat flow into work. The striking conclusion we will prove in Chapter 4 is that it is impossible to convert all of the heat flow from the hot reservoir into work at reasonable temperatures. From an overall perspective, the detailed steps of the Carnot engine can be ignored. The amount of work is given by Eqn. 3.6. We can simply state that heat comes in, heat goes out, and the difference is the net work. This situation is represented by Fig. 3.2(a). As an alternate perspective, any process with a finite temperature gradient should produce work. If it does not, then it must be irreversible, and “wasteful.” This situation is represented by Fig. 3.2(b). These observations are similar to previous statements about gradients and irreversibility, but Eqn. 3.6 establishes a quantitative connection between the temperature difference and the reversible work possible.
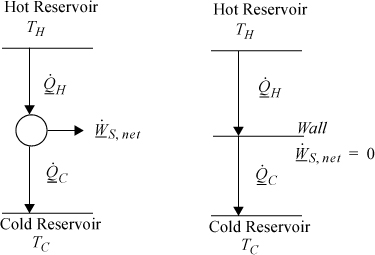
Figure 3.2. The price of irreversibility. (a) Overall energy balance perspective for the reversible heat engine. (b) Zero work production in a temperature gradient without a heat engine, QH = QC.
We will demonstrate in Chapter 4 that the Carnot thermal efficiency matches the upper limit attainable by any feasible process using heat flow as the source of work. On the other hand, it is not necessarily true that every engine is a heat engine. For instance, a fuel cell could conceivably convert the chemical energy of gasoline into electricity and then power a motor from the electricity. Fuel cells are not bound by the constraints of the Carnot cycle because they are not dependent on heat as the energy source. Also, not all engines operate between constant temperature reservoirs, so the direct comparison with the Carnot cycle is not possible.
Carnot Heat Pump
Suppose that we decided to reverse every step in the Carnot cycle. All the state variables would be the same, but all the heat and work flows would change signs. Instead of producing work, the process would require work, but it would absorb heat from a cold reservoir and reject heat to a warm reservoir. A Carnot heat pump may be used as a refrigerator/freezer or as a heater depending on whether the system of interest is on the cold or warm side of the heat pump. In a refrigeration system, the goal is to remove heat from the cold area and reject it to the warmer surroundings. Heat pumps can be purchased for home heating, and in that mode, they can extract heat from the colder outdoors and “pump” it to the warmer house.
A Carnot heat pump results from running a heat engine backwards.
For a given transfer of heat from the cold reservoir, a Carnot heat pump requires the minimum amount of work for any conceivable process. The coefficient of performance, COP, is the ratio of heat transferred from the cold reservoir to the work required. COP is a mirror image of thermal efficiency, reappearing in Units I and II. We want to maximize COP when the objective is to cool a refrigerator with as little work as possible.
Eqn. 3.5 has a subtle inversion of volumes that drops out:
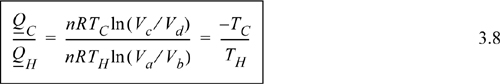
Eqn. 3.3 still applies, and the COP is given by
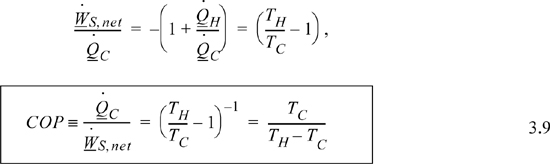
Example 3.1. Analyzing heat pumps for housing
Suppose your family is considering replacing your furnace with a heat pump. Work is necessary in order to “pump” the heat from the low outside temperature up to the inside temperature. The best you could hope for is if the heat pump acts as a reversible heat pump between a heat source (outdoors in this case) and the heat sink (indoors). The average winter temperature is 4°C, and the building is to be maintained at 21°C. The coils outside and inside for transferring heat are of such a size that the temperature difference between the fluid inside the coils and the air is 5°C. We generally refer to this as the approach temperature. What would be the maximum cost of electricity in ($/kW-h) for which the heat pump would be competitive with conventional heating where a fuel is directly burned for heat. Consider the cost of fuel as $7.00 per 109J, and electricity as $0.10 per kW-h. Consider only energy costs.
Solution
The Carnot heat pump COP, Eqn. 3.9
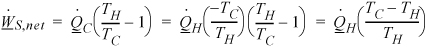
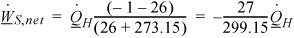
where 
is the heating requirement in kW. Heat pump operating 
, where θ is an arbitrary time and x is the cost.
Direct heating operating 
For the maximum cost of electricity for competitive heat pump operation, let heat pump cost = direct heating cost at the breakeven point.
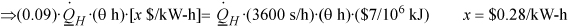
Since the actual cost of electricity is given as $0.10/kW-h it might be worthwhile if the heat pump is reversible and does not break down. (Purchase, installation, and maintenance costs have been assumed equal in this analysis, although the heat pump is more complex.)
Leave a Reply