Fundamental Concepts of Chemical Engineering Kinetics

The essence of reactor design is obtaining economically optimum specifications for a reactor for a specified duty. For example, let us assume that the market demand for a certain chemical product (let us denote it by R) is 3000 tons per year. The specified duty then might be defined as a production rate of 10 tons per day (tpd) of that chemical, assuming 300 working days every year. The challenge for the chemical engineer, at a very basic level, is finding the optimum volume of the reactor and reaction time that will yield this specified output of product R, starting from another chemical A, which is the raw material or reactant for the process. This situation is shown in Figure 9.1.

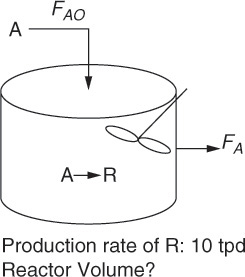
Figure 9.1 A simple chemical reactor design problem.

Adapted from: Fogler, H. S., Elements of Chemical Reaction Engineering, Fourth Edition, Prentice Hall, Upper Saddle River, New Jersey, 2004.

The principles of material balance and information on the stoichiometry of the reaction are used to calculate the material requirements for the process, as discussed in Chapter 6, “Material Balance Computations.” This information is necessary, but not sufficient, for reactor design. The approach to reactor design, incorporating the principles of chemical engineering kinetics, is based on the component material balances. The generalized component material balance for any species i, written in terms of molar quantities, is shown by equation 9.1.

In this equation, F_i,in and F_i,out represent the molar flow rates of i entering and leaving the reactor having volume V, respectively. N_i are the moles of the species present in the reactor, and the left side of the equation represents the rate of change of moles of i in the reactor, and r_i is the volumetric rate of generation of moles of i. The last term, which is the product of the reactor volume and the volumetric rate of generation of i, yields the molar rate of generation of i in the reactor. Thus equation 9.1 simply is the mathematical expression stating that the rate at which moles of i changing with time is equal to the difference in the inlet and outlet molar flow rates added to the molar rate of generation of the species i from the reaction.

The intrinsic kinetics of the reaction involves quantification of the rate of reaction r_i and its dependence on properties of chemical species involved in the reaction. As mentioned earlier, this intrinsic kinetics is combined with the reactor behavior for reactor design. The basic principles of both these aspects, the intrinsic kinetics and the reactor behavior, constitute the concepts of chemical engineering kinetics and are described in the following section.