There is a simple way that a force on a surface may interact with the system to cause expansion/contraction of the system in volume. This is the type of surface interaction that occurs if we release the latch of a piston, and move the piston in/out while holding the cylinder in a fixed location. Note that a moving boundary is not sufficient to distinguish this type of work—there must be movement of the system boundaries relative to one another. For expansion/contraction interactions, the size of the system must change. This distinction becomes significant when we contrast expansion/contraction work to flow work in Section 2.3.
How can we relate this amount of work to other quantities that are easily measured, like volume and pressure? For a force applied in the x direction, the work done on our system is
dW = Fapplied dx = –Fsystem dx
where we have used Newton’s principle of equal and opposite forces acting on a boundary to relate the applied and system forces. Since it is more convenient to use the system force in calculations, we use the latter form, and drop the subscript with the understanding that we are calculating the work done on the system and basing the calculation on the system force. For a constant force, we may write
W = – FΔx
If F is changing as a function of x then we must use an integral of F,

For a fluid acting on a surface of constant area A, the system force and pressure are related,
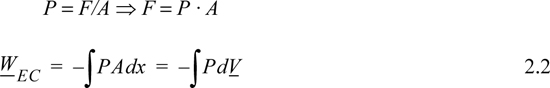
where the subscript EC refers to expansion/contraction work.
In evaluating this expression, a nagging question of perspective comes up. It would be a trivial question except that it causes major headaches when we later try to keep track of positive and negative signs. The question is essentially this: In the discussion above, is positive work being done on the system, or is negative work being done by the system? When we add energy to the system, we consider it a positive input into the system; therefore, putting work into the system should also be considered as a positive input. On the other hand, when a system does work, the energy should go down, and it might be convenient to express work done by the system as positive. The problem is that both perspectives are equally valid—therefore, the choice is arbitrary. Since various textbooks choose differently, there is always confusion about sign conventions. The best we can hope for is to be consistent during our own discussions. We hereby consider work to be positive when performed on the system. Thus, energy put into the system is positive. Because volume decreases when performing work of compression, the sign on the integral for work is negative,
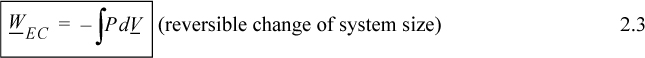
where P and V are of the system. Clarification of “reversible” is given in Section 2.4 on page 42. By comparing Eqn. 2.3 with the definitions of work given by Eqns. 2.1 and 2.2, it should be obvious that the dV term results from expansion/contraction of the boundary of the system. The P results from the force of the system acting at the boundary. Therefore, to use Eqn. 2.3, the pressure in the integral is the pressure of the system at the boundary, and the boundary must move. A system which does not have an expanding/contracting boundary does not have expansion/contraction work.1
Leave a Reply