The energy balance for systems involving a simple flow of a fluid is characterized by the lack of conversion of chemical, thermal, or any other kind of energy into mechanical energy. Essentially, the resulting mathematical formulation is simply a mechanical energy balance wherein the energy contributions arise from the potential and kinetic energy terms and flow work [3]. For an incompressible (constant density) fluid that does not experience any friction, the mechanical energy balance is given by equation 5.1 [1]:

where P is the pressure, V is the velocity, ρ is the density of the fluid, and z is the elevation of the fluid in the gravitational field, g being the acceleration due to gravity. The terms in the equation have the units of J/kg (energy per unit mass), and this equation is known as the Bernoulli equation [1]. The validity of the Bernoulli equation is limited to frictionless flow, but in reality, frictional effects need to be accounted for. Applying the Bernoulli equation between points 1 and 2 yields equation 5.2 [1]:
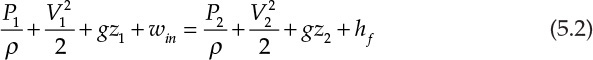
where hf represents the frictional losses. It is assumed that the fluid flow is accomplished by means of a pump between the two points, and win is simply the work input from this pump. It should be clear from equation 5.2 that the power requirement for transferring a fluid from one point to another depends on the following four factors:2
2. A student will encounter the detailed analysis while conducting the mechanical energy balance in later curriculum.
• The difference in the hydrostatic pressure between the two points
• The difference in the elevation of the two points
• The difference between the fluid velocities at the two points
• The frictional losses in the piping system
The frictional losses depend on the flow regime, and the accounting of the frictional losses requires an understanding of the concept of viscosity.
Leave a Reply