Roughly 80% of separations are conducted by distillation and a significant portion of the energy involved in the global chemical process industries is devoted to distillation. Why are more distillation columns needed than reactors? Reactors rarely run to 100% conversion and rarely produce a single product with 100% purity. There may be a by-product of the primary reaction or a solvent reaction medium. Additionally, there may be side reactions that can be minimized but not eliminated. Altogether, the reactor effluent almost always contains several components, and products need to be separated to high purity before they can be sent out of the process or recycled.
Analyzing distillation is important for a more philosophical reason as well. It is a common unit operation that involves mass and energy balances, heat and mass transfer, and phase partitioning. This kind of analysis pervades chemical engineering in general. The important consideration is the thought process that leads to the model equations. That thought process can be applied to any system, no matter how complex. As we proceed through the analysis distillation, try to imagine how you might develop similar approximations for other systems. Challenge yourself to anticipate the next step in every derivation. In the final analysis, your skill at developing simple models of complex phenomena is more valuable than memorizing model equations developed by somebody else.
We will address the phase equilibrium aspects of distillation in Section 10.6 on page 390, and you may wish to skim that section now. Briefly, the fraction with the lowest boiling point rises in the column and the fraction with the highest boiling point flows to the bottom. In this section, the focus is on mass and energy balances for distillation. A common model in distillation column screening is called constant molar overflow. In this model, the actual enthalpy of vaporization of a mixture is represented by the average enthalpy of vaporization, which can be assumed to be independent of composition for the purposes of this calculation, ![]() . Also, all saturated liquid streams are considered to have the same enthalpy, and all saturated vapor streams are considered to have the same enthalpy. These assumptions may seem extreme, but the model provides an excellent overview of key operating conditions.
. Also, all saturated liquid streams are considered to have the same enthalpy, and all saturated vapor streams are considered to have the same enthalpy. These assumptions may seem extreme, but the model provides an excellent overview of key operating conditions.
In the constant molar overflow model for a column with one feed, the column may be represented by five sections as shown in Fig. 3.3: a feed section where the feed enters; a rectifying section above the feed zone; a condenser above the rectifying section which condenses the vapors and returns a portion of the liquid condensate as reflux LR to ensure that liquid remains on the trays to induce the liquid-vapor partitioning that enhances the compositions.; a stripping section below the feed section; and a reboiler that creates vapors from the liquid flowing down the column.
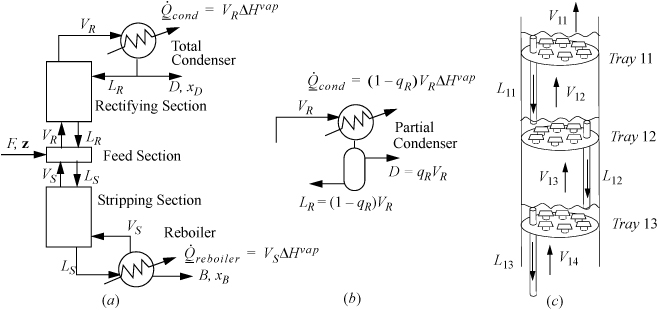
Figure 3.3. (a) Overall schematic of a distillation column with a total condenser showing five sections of a distillation column. and conventional labels; (b) a partial condenser; (c) schematic of liquid levels on bubble cap trays with the downcomers used to maintain the liquid levels.
At the bottom of the column, heat is added in the reboiler, causing vapor to percolate up the column until it reaches the condenser. The heat requirement in the reboiler is called the heating duty. B is called the bottoms or bottoms product. The ratio VS/B is called the boilup ratio. The energy requirement of the reboiler is known as the reboiler duty and is directly proportional to the moles of vapor produced as shown in the figure.
At the top of the column, Fig. 3.3(a) shows a total condenser where the vapor from the top of the column is totally condensed. The liquid flow rate leaving the condenser will be VR = (LR + D). D is called the overhead product or distillate. LR is called the reflux. The proportion of reflux is characterized by the reflux ratio, R = LR/D. A partial condenser may also be used as shown in (b), and the overhead product leaves as a vapor and the condensed fraction is the reflux. The cooling requirement of the condenser is called the condenser duty and the duty depends on whether the condenser is total or partial as shown in the figure.
The rectifying and stripping sections of the column have either packing or trays to provide retention of the liquid and contact with vapors. Trays are easier to introduce as shown in Fig. 3.3(c). At steady state, each tray holds liquid and the vapor flows upwards through the liquid. The trays can be constructed with holes (sieve trays) or bubble caps (bubble cap trays) or valves (valve trays). The bubble caps sketched in the figure represent a short stub of pipe with a short inverted “cup” called the “cap” with slots in the sides (slots are not shown) supported with spacing so that vapor can flow upwards through the pipe and out through the slots in the cap. A downcomer controls the liquid level on the tray as represented by a simple pipe extending above the surface of the tray in the figure. and in an ideal column each tray creates a separation stage. Using multiple stages provides greater separation. By stacking the stages, rising vapor from a lower stage boils the liquid on the next stage. At steady state, streams VS and VR are assumed to be saturated vapor unless otherwise noted. Streams B, LS, and LR are assumed to be saturated liquid unless otherwise noted. D is either assumed to be either a saturated liquid or a vapor depending on whether the condenser is total or partial, respectively. According to the constant molar overflow model, at steady state the vapor and liquid flow rates are constant within the stripping and rectifying sections because all the internal streams in contact are saturated, and change only at the feed section as determined by mass and energy balances around the feed section.
One of the most challenging tasks in the undergraduate chemical engineering laboratory is to explain the dynamics of the distillation column during start-up. Students tend to assume that the entire distillation column starts working as soon as heat is applied to the reboiler. However, during column start-up, the internal flows are not constant in the column sections. Heat moves up the column one tray at a time as boiling vapor leaves one tray and enters another. Consider Fig. 3.3(c). When tray 12 starts to boil, rising vapors will be condensed by the cold liquid on tray 11 immediately above and by the cold column. In principle, the vapor flow leaving the upper tray 11, V11, will be approximately zero until the column and liquid on the tray reaches the saturation temperature of the liquid on tray 11. Vapors reaching tray 11 are condensed and give up latent heat. Then tray 11 begins to warm. The condensed vapors create liquid overflow of subcooled liquid from tray 11 back down to tray 12. The lower tray 12 continues to boil, but the cool downcomer liquid causes the vapor rate V12 to be smaller than V13. Tray 12 stays at a fairly constant temperature as it continues to boil because it stays saturated. Finally, when tray 11 begins to boil, the process repeats for tray 10 and so on.
This introduction is not intended to explain every detail of distillation and energy balances, but it should suffice for you to deduce the most important qualitative behaviors. An illustration of the kinds of possible inferences is given in Example 3.2. Homework problem 3.4 provides additional exercises related to steady-state distillation.
Example 3.2. Start-up for a distillation column
A particular bubble cap distillation column for methanol + water has 12 trays numbered from top to bottom. Each tray is composed of 4 kg of materials and holds 1 kg of liquid. The heat capacity of the tray materials is 6 J/g-K and the heat capacity of the liquid is 84 J/mol-K = 3.4 J/g-K. During start-up, the feed is turned off. Roughly 15 minutes after the reboiler is started, tray 12 has started to boil and the temperature on tray 11 begins to rise. The reboiler duty is 6 kW and the heat loss is negligible. Tray 11 starts at 25 °C and the temperature of the liquid and the tray materials is assumed the same during start-up. Assume the liquid inventory on Tray 11 is constant throughout start-up.
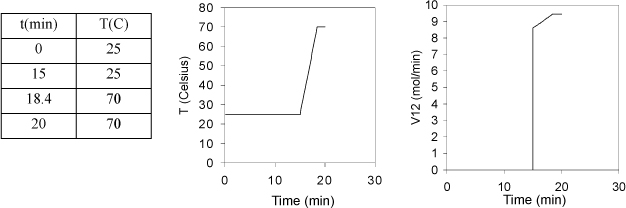
a. Tabulate and plot the temperature versus time for tray 11 until it starts to boil at 70 °C.
b. Plot the vapor flow V12 as a function of time.
Solution
a. First, recognize that V11 = 0 since tray 11 is subcooled. No liquid is flowing down to tray 11. L10 = 0 since F = 0 and no vapors are being condensed yet (LR = 0), even though the cooling water may be flowing.
Mass balance on tray 11 (all vapors from below are being condensed during start-up, V11 = 0, L10 = 0):

Mass balance on boundary around tray 11 + tray 12 (V11 = 0, L10 = 0, during start-up):

State 11 is subcooled during start-up and will warm until T11 = 70:
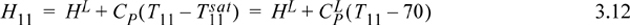
Energy balance on tray 11 during start-up (no work, no direct heat input, energy input by flow of hot vapors, negligible heat loss):
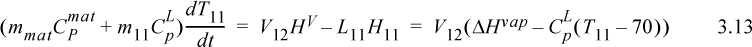
where for the last equality we have inserted Eqn. 3.10 and then Eqn. 3.12.
An energy balance on tray 12 (which is at constant temperature) gives:
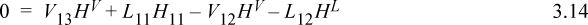
Using Eqn. 3.12 to eliminate H11, Eqn. 3.10 to eliminate L11, and Eqn. 3.11 to eliminate L12,
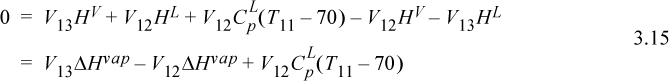
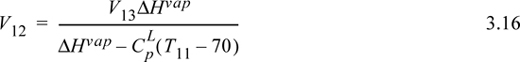
Inserting Eqn. 3.15 into Eqn. 3.13, and recognizing the constant vapor flow rate below tray 13,
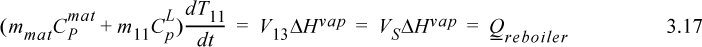
where ‘mat’ indicates column material. Inserting values from the problem statement gives,
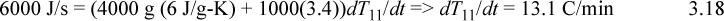
The tray will require approximately (70 – 25)/13.1 = 3.4 min to reach saturation temperature. The plot is shown below.
b. The vapor flow is given by Eqn. 3.13 using T11 = 25 + 13.1(t – 15). The average heat of vaporization is (40.7 + 35/3)/2 = 38 kJ/mol. Between 15 and 18.4 min, the flow rate in mol/min
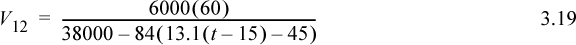
Note that we neglect details like imperfect mixing or bypass heating (vapor that does not get condensed) that would round the edges of the temperature profile.
Note that as soon as vapors start to reach tray 11 in Example 3.2 the net energy input is constant even though the flow rate of hot vapors into the tray is increasing with time during start-up. Why? The answer is that energy is also being transported away from the tray by the flow down the downcomer. As the tray warms, this energy transport out is increasing at the same rate as the increased energy transport into the stage by the increasing flow of vapor. Analysis of subtleties such as this will deepen your understanding of physical phenomena and your appreciation for the utility of the energy balance.
3.3. Introduction to Mixture Properties
The previous section used “average” properties for the streams. This level of approximation is too crude for most calculations. We therefore need to understand how to estimate mixture properties.
Property Changes of Mixing
Communication of the property changes is facilitated by defining the property change of mixing as the mixture property relative to the mole-fraction weighted sum of the component properties in the unmixed state. Using x to be a generic composition variable, the energy of mixing is

The enthalpy of mixing is:

The volume of mixing is the volume of the mixture relative to the volumes of the components before mixing.

Similar equations may be written for other properties that we will define later: entropy of mixing, Gibbs energy of mixing, and Helmholtz energy of mixing – but these must reflect the increased disorder inherent in creating mixtures from pure fluids. If the property change on mixing (e.g., ΔHmix) has been measured and correlated in a reference book or database, we can use it to calculate the stream property at a later time:



Leave a Reply