Generally, the strategies discussed in Section 2.14 are sufficient to simplify the energy balance. Occasionally, in applying the energy balance to a new type of system, simplification of the balances may require more detailed analysis of the background leading to the terms and/or details of interactions at boundaries. This section provides an overall summary of the details for the principles covered earlier in this chapter, and it is usually not necessary unless you are having difficulty simplifying the energy balance and need details regarding the meaning of each term.
The universe frequently consists of three subsystems, as illustrated in Fig. 2.10. The container (System 2) is frequently combined with System 1 (designated here as System (1 + 2)) or System 3 (designated here as System (2 + 3)). For every balance, all variables are of the system for which the balance is written,
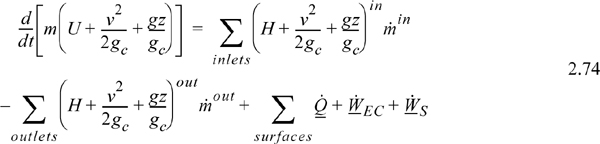
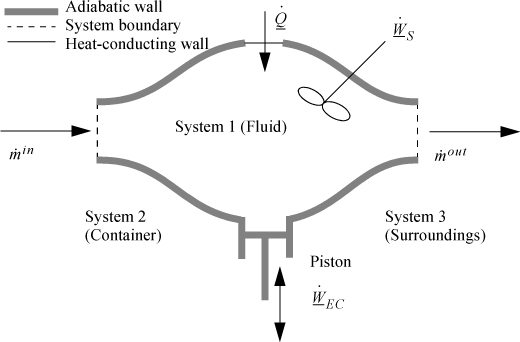
Figure 2.10. Schematic of a general system.
where superscripts “in” and “out” denote properties of the streams which cross the boundaries, which may or may not be equal to properties of the system.
1. Non-zero heat interactions of Systems 1 and 3 are not equal unless the heat capacity or mass of System 2 is negligible.
2. Hout, Hin account for internal energy changes and work done on the system due to flow across boundaries.
3. ![]() represents work done on the system due to expansion or contraction of system size. Fboundary is the absolute value of the system force at the boundary. (By Newton’s third principle, the forces are equal but act in opposite directions at any boundary.) Note that system 1 and system 3 forces are not required to be equal. Unequal forces create movement (acceleration) of any movable barrier (e.g., piston head).
represents work done on the system due to expansion or contraction of system size. Fboundary is the absolute value of the system force at the boundary. (By Newton’s third principle, the forces are equal but act in opposite directions at any boundary.) Note that system 1 and system 3 forces are not required to be equal. Unequal forces create movement (acceleration) of any movable barrier (e.g., piston head).
4. ![]() represents the work done on the system resulting from mechanical forces at the surface of the system except work due to expansion/contraction or mass flow across boundaries. Turbines and compressors are part of system 2; thus they are involved with work interactions with the fluid in system 1. Note that piston movement is calculated as
represents the work done on the system resulting from mechanical forces at the surface of the system except work due to expansion/contraction or mass flow across boundaries. Turbines and compressors are part of system 2; thus they are involved with work interactions with the fluid in system 1. Note that piston movement is calculated as ![]() for systems 1, 3, (1+2), or (2+3), but the movement is calculated as
for systems 1, 3, (1+2), or (2+3), but the movement is calculated as ![]() for system 2 alone. When a balance for system 2 is considered, the movement of the piston is technically shaft work, even though no shaft is involved. (The piston is a closed system, and it does not expand or contract when it moves.) As another example of the general definition of shaft work as it relates to forces at the surface of a system, consider the closed system of Fig. 2.3 on page 48 being raised 150 m or accelerated to 75 m/s. There is a work interaction at the surface of the system required for these energy changes even though there is not a “rotating” shaft.
for system 2 alone. When a balance for system 2 is considered, the movement of the piston is technically shaft work, even though no shaft is involved. (The piston is a closed system, and it does not expand or contract when it moves.) As another example of the general definition of shaft work as it relates to forces at the surface of a system, consider the closed system of Fig. 2.3 on page 48 being raised 150 m or accelerated to 75 m/s. There is a work interaction at the surface of the system required for these energy changes even though there is not a “rotating” shaft.
5. Non-zero ![]() or
or ![]() interactions of systems 1 and 3 are not equal unless changes in kinetic and potential energy of the moving portion of system 2 (e.g., piston head for
interactions of systems 1 and 3 are not equal unless changes in kinetic and potential energy of the moving portion of system 2 (e.g., piston head for ![]() or turbine for
or turbine for ![]() ) are negligible and the movement is reversible.
) are negligible and the movement is reversible.
6. Frictional forces, if present, must be attributed to one of the systems shown above. Irreversibility due to any cause does not require additional energy balance terms because energy is always conserved, even when processes are irreversible.
7. Electrical and magnetic fields have not been included.
8. On the left-hand side of the equation, kinetic and potential energy changes are calculated based on movement of the center of mass. In a composite system such as (1+2), they may be calculated for each subsystem and summed.
Leave a Reply