To apply the relationships that we can develop for relating changes in properties to CP, CV, P, T, V, and their derivatives, we need really general relationships between P, V, and T. These relationships are dictated by the equation of state (EOS). Constructing an equation of state with a firm physical and mathematical foundation requires considering how the intermolecular forces affect the energy and pressure in a fluid. In a dense fluid, we know that the molecules are close together on the average, and such closeness gives rise to an attractive potential energy. A common practical manifestation of this attractive energy is the heat of vaporization of a boiling liquid. But how can we make a quantitative connection between molecular forces and macroscopic properties? A firm understanding of this physical and mathematical foundation is helpful to understand the extensions to multicomponent mixtures and multiphase equilibria. A proper derivation would provide a mathematical connection between the microscopic potential and the macroscopic properties. We will lay the groundwork for such a rigorous derivation later in the chapter. For introductory purposes, however, we would like to see how some typical equations look and how to use them in conjunction with the theorem of corresponding states.
The van der Waals Equation of State
One of the most influential equations of state has been the van der Waals (1873) equation. Even the most successful engineering equations currently used are only minor variations on the theme originated by van der Waals. The beauty of his model is that detailed knowledge of the molecular interactions is not necessary. Simply by noting that there are two characteristic molecular quantities (ε and σ) and two characteristic macroscopic quantities (Tc and Pc), he was able to infer a simple equation that captured the key features of each fluid through the principle of corresponding states. His final equation expressed the attractive energy in terms of a parameter which he referred to as a, and the size parameter b, but the choice of symbols was arbitrary. The key feature to recognize at this stage is that there are at least two parameters in all the equations and that these can be determined by matching experimental data.
Johannes Diderik van der Waals (1837–1923) was a Dutch physicist. He was awarded the 1910 Nobel Prize in physics.
The resulting equation of state is:
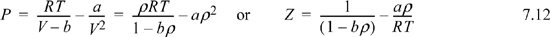
where ρ = molar density = n/V.
Note: Common engineering practice is to use ρ to denote intensive density. We follow that convention here, using ρ as molar density. Advanced chemistry and physics books and research publications frequently use ρ as number density N/V = nNA/V, so the definitions must be carefully determined.
ρ will be used to denote molar density.
The exact manner of determining the values for the parameters a and b is discussed in Section 7.8 on page 270.
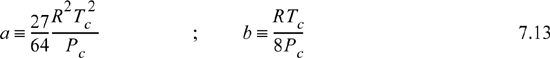
We may write the equation of state as Z = 1 + Zrep + Zatt, where 1 denotes the ideal gas behavior, Zrep represents the deviations from the ideal gas law due to repulsive interactions, Zatt represents the deviations due to attractive interactions. For the van der Waals equation,
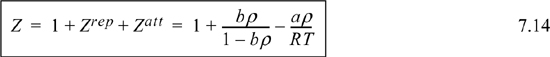
The van der Waals equation written in the form Z = 1 + Zrep + Zatt.
where the second and third terms on the right-hand side are Zrep and Zatt, respectively. Eqn. 7.12 is compact, but Eqn. 7.14 more clearly represents the origin of the contributions to Z. In many later applications we will need to use the departure of Z from ideal gas behavior, Z–1, and Eqn. 7.14 will fulfill this need. There are two key features of the van der Waals equation. First, note that the repulsive term accounts for the asymptotic divergence of the compressibility factor as the packing factor bρ increases. The divergence occurs because rapidly increasing large pressures are required to increase the density as close packing is approached. Second, note that the attractive term increases in magnitude as the temperature decreases, and contributes to smaller values of Z at low T. The contributions of the attractive forces increase at low temperature because the kinetic energy can no longer overwhelm the potential attractions at low temperature. As we have discussed, this eventually leads to condensation. The discussion in Section 7.11 provides a better understanding of the molecular basis of the van der Waals equation. Note that the van der Waals EOS does not incorporate the acentric factor and is incapable of representing different vapor pressure slopes. It is thus primarily a pedagogical tool to introduce the forms of cubic EOSs, not a practical tool.
The Peng-Robinson Equation of State
Since the time of van der Waals (1873), many approximate equations of state have been proposed. For the most part, these have been semi-empirical corrections to van der Waals’ characterization of “a = constant,” and most have taken the form a = a(T,ω). One of the most successful examples of this approach is that of Peng and Robinson (1976). We refer to this equation many times throughout this text and use it to demonstrate many central themes in thermodynamics theory as well as useful applications.
The Peng-Robinson EOS. Note that a is a temperature-dependent parameter, not a constant. Note the dependence on the acentric factor.
The Peng-Robinson equation of state (EOS) is given by:
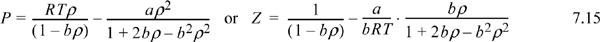
where ρ = molar density = n/V, b is a constant, and a depends on temperature and acentric factor,7
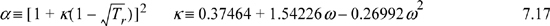
Note that α is not the isobaric coefficient of thermal expansion and κ is not the isothermal compressibility – they are simply variables introduced by Peng and Robinson for notational convenience. The temperature derivative of a is useful when temperature derivatives of Z are needed:
Tc, Pc, and ω are reducing constants according to the principle of corresponding states. Expressing the contributions to Z in the manner we followed for the van der Waals equation,
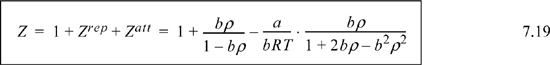
Comparison of the Peng-Robinson equation to the van der Waals equation shows one obvious similarity; the repulsive term is the same. There are some differences: the temperature dependence of the attractive parameter a is incorporated; dependence of a on the acentric factor is introduced; and the density dependence of Zatt is altered by the denominator of the attractive term. The manner in which these extra details were added was almost entirely empirical; different equations were tried until one was found which seemed to fit the data most accurately while retaining cubic behavior. (Many equations can be tried in 103 years.) There is not much to say about this empirical approach beyond the importance of including the acentric factor. The main reason for the success of the Peng-Robinson equation is that it is primarily applied to vapor-liquid equilibria and that the representation of vapor-liquid equilibria is strongly influenced by the more accurate representation of vapor pressure implicit in the inclusion of the acentric factor. Since the critical point and the acentric factor characterize the vapor pressure fairly accurately, it should not be surprising that the Peng-Robinson equation accurately represents vapor pressure.
There are a lot of EOSs. We focus on the Peng-Robinson to illustrate the concepts.
One caution is given. The differences in accuracy between various equations of state are subtle enough that one equation may be most accurate for one narrow range of applications, while another equation of state is most accurate over another range. This may require a practicing engineer to adopt an equation of state other than the Peng-Robinson equation for his specific application. Nevertheless, the treatment of the Peng-Robinson equation presented here is entirely analogous to the treatment required for any equation of state. If you understand this treatment, you should have no problem adapting. A brief review of several thermodynamic models commonly encountered in chemical process simulations is given in Appendix D.
Note: The variables a and b are used throughout equation of state literature (and this text) to denote equation of state parameters. The formulas or values of these parameters for a given equation of state cannot be used directly with any other equation of state.
The variables a and b are commonly used in EOSs. Do not interchange the formulas.
7.6. Solving the Cubic Equation of State for Z
In most applications we are given a pressure and temperature and asked to determine the density and other properties of the fluid. This becomes slightly difficult because the equation involves terms of density that are to the third power (“cubic”) even when simplified as much as possible. Standard methods for solutions to cubic equations can be applied. The equation can be made dimensionless prior to application of the solution method. Note:
Dimensional analysis is an important engineering tool. Here we make the EOS dimensionless so that it can be solved in a generalized way.
Defining dimensionless forms of the parameters
results in the lumped variables
The Peng-Robinson equation of state becomes
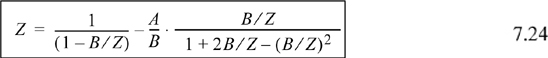
Do not confuse the EOS parameters A and B with other uses of the variables. The intended use is almost always clear.
Note: The variable A is also used elsewhere in the text to denote Helmholtz energy. The variable B is used elsewhere in the text to represent the second virial coefficient and availability. The context of the variable usage should make the meaning of the variable clear. We choose to use A and B as reduced equation of state parameters for consistency with equation of state discussions in the literature.
Rearranging the dimensionless Peng-Robinson equation yields a cubic function in Z that must be solved for vapor, liquid, or fluid roots:
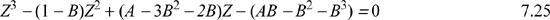
Isotherm Shape and the Real Roots
Fig. 7.5 shows several P-V isotherms for CO2 as generated with Eqn. 7.15. Comparing to Fig. 1.4, note that the cubic EOS predicts “humps” when T < Tc. The humps are larger at lower temperature, and the pressure can be negative as shown by the 275 K isotherm. The cubic equation always has three roots, but at some conditions two are imaginary roots. For engineering, we are interested in the real roots. For the isotherm at 290 K, three real roots exist at pressures between approximately 39 bar and 58 bar. We will refer to this pressure region as the three-root region meaning that there are three real roots in this region. Above 58 bar, only a liquid root will result, and below 39 bar only a vapor root will result. These two regions are called one-root regions to communicate that only one real root exists in this region. The three-root region size depends on temperature. At 275 K the three-root region extends down to P = 0, but the region is very narrow near 300 K.
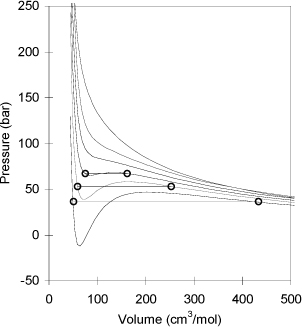
Figure 7.5. Illustration of the prediction of isotherms by the Peng-Robinson equation of state for CO2 (Tc = 304.2 K) at 275 K, 290 K, 300 K, 310 K, 320 K, and 350 K. Higher temperatures result in a high pressure for a given volume. The “humps” are explained in the text. The calculated vapor pressures are 36.42 bar at 275 K, 53.2 bar at 290 K, and 67.21 bar at 300 K.
The cubic equation for Z in Eqn. 7.25 also has similar behavior. Naming this function F(Z), we can plot F(Z) versus Z to gain some understanding about its roots as shown in Fig. 7.6. Considering the case when P = Psat, we see that three real roots exist; the larger root of F(Z) will be the vapor root and will be the value of Z for saturated vapor. The smallest root will be the liquid root and will be the value of Z for saturated liquid. At all other pressures at this temperature, where three real roots are found, one of the roots is always more stable. Below the critical temperature, when P > Psat, the fluid will be a compressed liquid, and the liquid root is more stable. Below the critical temperature, when P < Psat, the fluid will be a superheated vapor and the vapor root is more stable. When T > Tc, we have a supercritical fluid which can only have a single root but it may vary continuously between a “vapor-like” or “liquid-like” densities and compressibility factors. We will discuss stability and how to choose the stable root without generating an entire isotherm in an upcoming section.
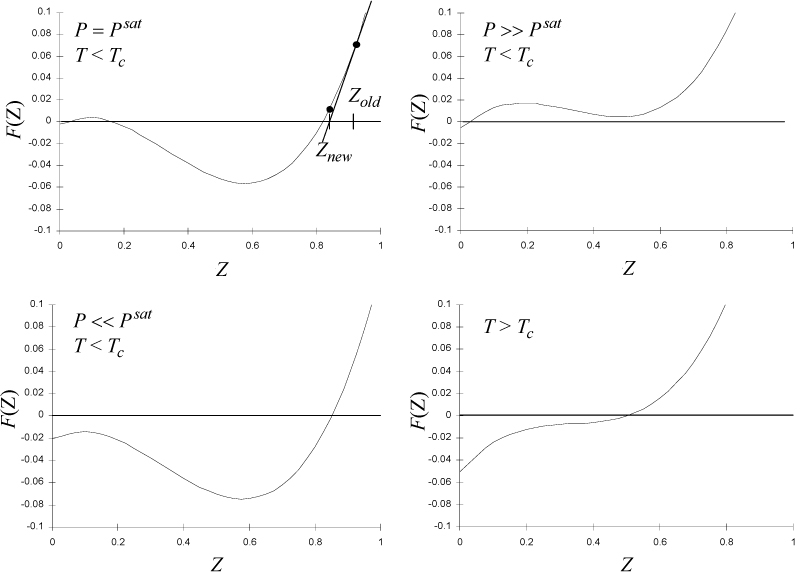
Figure 7.6. Comparison of behavior of cubic in Z for the Peng-Robinson equation of state at several conditions. The labels Znew and Zold in the upper left are described in the iterative description in Appendix B.
Methods of Solving the Cubic Equation
Engineering applications typically specify P and T, and require information about V. Solution of the equation of state in terms of Z is preferred over solution for V, and we can subsequently find V using
The value of Z often falls between 0 and 1. (See Fig. 7.4 on page 257.) V often varies from 50–100 cm3/mole for liquids to near infinity for gases as P approaches zero. It is much easier to solve for roots over the smaller variable range using the compressibility factor Z. There are two basic approaches to solving cubic equations of state. First, we may use an iterative method. One such method is the Newton-Raphson method. Another method is to solve analytically. A computer or calculator program is helpful in either solution method.
Iterative Method
The Newton-Raphson method is described in Appendix B. The Newton-Raphson method uses an initial guess along with the derivative value to rapidly converge on the solution.
Analytical Solution
The other choice we have for solution of the cubic is to analytically obtain the roots as detailed in Appendix B. The method varies depending on whether one or three roots exist at the pressure of interest. Solutions are implemented in a spreadsheet (Preos.xlsx) or a MATLAB script (Preos.m). MATLAB includes a polynomial root finder, so the statement Zvals=roots([1 a2 a1 a0]) results in both real and imaginary roots. The argument in the “roots” function is the vector of coefficients for the polynomial in Z. In MATLAB, the indexes of the real roots can by found with index=find(imag(Zvals)==0) followed by selecting the real parts of the roots using Zreal=real(Zvals(index)).
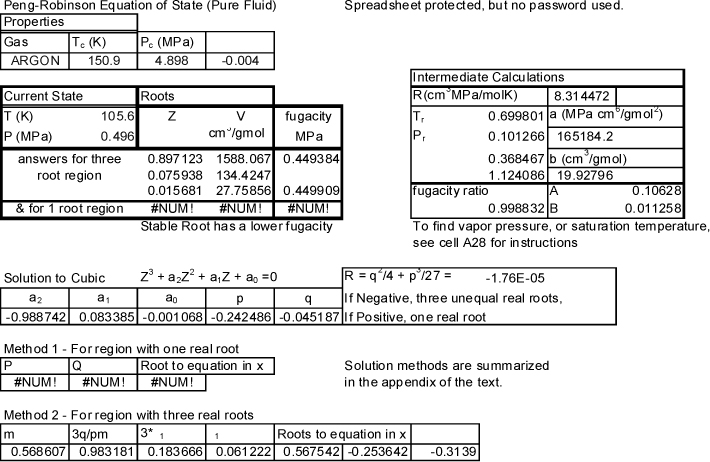
Preos.xlsx uses the procedures from Appendix B and shows the intermediate calculations.
Example 7.3. Peng-Robinson solution by hand calculation
Perform a hand calculation of the real roots for argon at 105.6 K and 0.498 MPa.
Solution
This example is available online and provides an example of hand calculation at the same conditions as the next example.
Example 7.4. The Peng-Robinson equation for molar volume
Find the molar volume predicted by the Peng-Robinson equation of state for argon at 105.6 K and 4.96 bar.
Solution
The critical data are entered from the table on the back flap of the text.
Preos.xlsx output is shown below. The state is in the three-root region, because the cells for the one-root region are labeled #NUM! by Excel. Many of the intermediate calculations are also shown. The volumes are 27.8, 134, and 1581 cm3/mole. The lower value corresponds to the liquid volume and the upper value corresponds to the vapor. Note that Z is close to zero for the liquid and close to one for the vapor.
The output from the Preos.m MATLAB script is also shown below. Though the default output does not include intermediate values, they may be obtained by removing the “;” at the end of any code line and rerunning the script.
Output from Preos.m:
argon Tc(K)= 150.9 Pc(MPa)= 4.898 w = -0.004
T(K)= 105.600000 P(MPa)= 0.496000
Zvals =
0.8971
0.0759
0.0157
Z= 0.897123 0.015681
V(cm^3/mol)= 1588.066740 27.758560
fugacity (MPa)= 0.449384 0.449903
Hdep (J/mol)= -222.933032 -6002.507074
Example 7.5. Application of the Peng-Robinson equation
Estimate the specific volume in cm3/g for carbon dioxide at 310 K and (a) 8 bars (b) 75 bars by the Peng-Robinson equation and compare to the experimental values of 70.58 and 3.90, respectively.1
Solution
ω = 0.228, Tc = 304.2, Pc = 73.82, MW = 44 g/gmol,
a. Z = 0.961
V = ZRT/(P · MW) = (0.961 · 83.14 · 310)/(8 · 44) = 70.37, within 0.3% of the experimental value.
b. Z = 0.492
V = ZRT/(P · MW) = (0.492 · 83.14 · 310)/(75 · 44) = 3.84 giving 1.5% error relative to the experimental value.
Example 7.5 shows the equation of state is much more reliable than reading the compressibility factor charts in Example 7.1 on page 258.
Determining Stable Roots
When three real roots are found, which is most stable can be quickly determined. As mentioned in Example 7.4, the smallest root usually corresponds to a liquid state, and the largest root usually corresponds to the vapor state.8,9 When three real roots are found over a range of pressures for a given temperature, these roots do not indicate vapor + liquid coexistence at all these conditions. Vapor and liquid phases coexist only at the vapor pressure—above the vapor pressure, the liquid root is most stable—below the vapor pressure, the vapor root is most stable. The most stable root represents the phase that will exist at equilibrium. When three roots are found, the most stable root has the lower Gibbs energy or fugacity. At phase equilibrium, the Gibbs energy and fugacity of the roots will be equal. Fugacity is closely related to the Gibbs energy and will be described in Chapter 9, but we will begin to use the calculated values before we explain the calculation procedures completely. When three roots exist, the center root is thermodynamically unstable because the derivative of pressure with respect to volume is positive, which violates our common sense, and is shown to be thermodynamically unstable in advanced thermodynamics texts. Physically, we can understand the meaning of the unstable root as follows. Imagine placing Lennard-Jones spheres all in a row such that the force pulling on each molecule from one direction is exactly balanced by the force in the other direction. Next, imagine placing similar rows perpendicular to that one until you obtain the desired density at the desired temperature. Physically and mathematically, this configuration is conceivable, but what will happen when one of these atoms moves? The perfect balance will be destroyed, and a large number of atoms will cluster together to form a liquid. The atoms that do not form a liquid will remain in the form of a low-density vapor. Although this discussion has discussed only the energy of interactions, the entropy is also important. It is actually a balance of enthalpy and entropy that results in phase equilibrium, as we will discuss in Chapter 9.
The stable root represents the phase that will exist at equilibrium. The stable root has the lower Gibbs energy or fugacity.
A simple way to visualize the conditions that lead to vapor-liquid equilibrium along an isotherm is to consider the P-V diagram illustrated in Fig. 7.5. We will show in Chapter 9 that the condition for equilibrium between vapor and liquid roots occurs when the horizontal line on the P-V diagram is positioned such that the area enclosed above the line is exactly equal to the area enclosed below the line. Even though the enclosed areas have different shapes, imagine moving this line up and down until it looks like the areas are equal. The dots in the figure are the predictions of the saturated liquid and vapor volumes, and form the phase envelope. The parts of the isotherms that are between the saturated vapor and saturated liquid roots are either metastable or unstable. To determine whether a given point is metastable or unstable, look for the point where the isotherm reaches a maximum or a minimum. Points between the liquid root and the minimum are considered metastable liquids; points between the maximum and the vapor root are considered metastable vapors. The metastable state can be experimentally obtained in careful experiments. Under clean conditions, it is possible to experimentally heat a liquid above its boiling point to obtain superheated liquid. Likewise, under clean conditions, it is possible (though challenging) to experimentally obtain subcooled vapor. However, a metastable state is easily disrupted by vibrations or nucleation sites, e.g., provided by a boiling chip or dust, and once disrupted, the state decays rapidly to the equilibrium state. The boundary between the metastable and unstable states is known as the spinodal condition, predicted by the EOS by the maximum and minimum in the humps in sub-critical isotherms. We will discuss more details about characterizing proper fluid roots when we treat phase equilibrium in a pure fluid.
Leave a Reply