Conversion

The discussion in section 9.1.3 assumes that the rate expression is dependent only on the concentration of one reactant, reactant A. However, in general, the rate depends on the concentrations of several other species as well. The component balance in equation 9.1 (and its simplifications discussed earlier) can be written for each species involved in the reaction, yielding as many equations in the species concentrations as the number of species. This will result in a large number of differential equations or algebraic/transcendental equations that need to be solved simultaneously for obtaining the species concentrations and hence determining the reactor volume, residence time, and batch time. The concept of conversion reduces this complexity by expressing concentrations of all the species in terms of a single variable and a single governing equation for reactor design.

Conversion (X) of the limiting reactant (reactant that would be consumed completely if the reaction were allowed to run its course) is simply the fraction of the reactant fed to the reactor that undergoes the reaction. If A is the limiting reactant, then in a batch system, we get the following:

Here, N_A0 and N_A are the moles of A present initially and those remaining after time t, respectively.

For a continuous reactor, the conversion is described in terms of molar flow rates (F_A0, F_A) instead of number of moles (N_A0, N_A). For a constant volume system, the conversion is related to the concentrations as follows:

The concentrations of all the other species (excess reactants, products) can then be expressed in terms of X_A using the reaction stoichiometry The system of equations is now reduced to a single governing equation that can be solved for X_A for a given reactor volume or for V when conversion is specified. For example, if the reaction can be represented by the following equation:

then, the concentration of B can be expressed in terms of conversion of the limiting reactant A by the following equation:

Here, ψ_B is the ratio of the initial concentrations of B and A (ψ_B = C_B0/C_A0). In general, the concentration of any species i is expressed using a similar expression [8]:

Here, v_i represents the stoichiometric coefficient of the species i in the reaction, and ψ_i is the ratio of the initial concentrations of i and A. It should be noted that the validity of equation 9.20 is restricted to constant-volume systems, and the reaction equation is written in the form Products − Reactants = 0; thus equation 9.18 is rearranged to read:

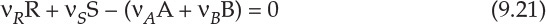
Typically, the approach to kinetic analysis involves developing a stoichiometric table [4], wherein the concentrations of various species are expressed in terms of concentration of the limiting reactant, its conversion, and initial concentration ratios (at time t = 0 for the batch reactor, and inlet of the reactor for PFR/CSTR). This development leads to equations 9.22, 9.23, and 9.24 that are the design equations for the batch reactor, CSTR, and PFR, respectively [4].

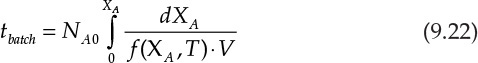
Depending on the information provided and the nature of the problems, these equations can be used to obtain reactor volumes, batch times, conversions in reactors of specified volumes, processing rates, and so on.