Several types of systems are quite common in chemical engineering practice. You need to be familiar with the results of their analysis and benefit if you memorize these results for rapid recall. You must simultaneously recall the assumptions underlying each simple model, however, to avoid incorrect applications.
Example 2.11. Adiabatic, reversible expansion of an ideal gas
Suppose an ideal gas in a piston + cylinder is adiabatically and reversibly expanded to twice its original volume. What will be the final temperature?
Solution
First consider the energy balance. The system will be the gas in the cylinder. The system will be closed. Since a basis is not specified, we can choose 1 mole. Since there is no mass flow, heat transfer, or shaft work, the energy balance becomes:
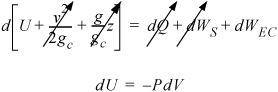
In this case, as we work down to step 4 in the strategy, we see that we cannot integrate the sides independently since P depends on T. Therefore, we need to combine terms before integrating.
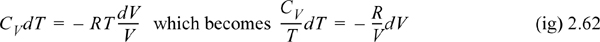
The technique that we have performed is called separation of variables. All of the temperature dependence is on the left-hand side of the equation and all of the volume dependence is on the right-hand side. Now, if we assume a constant heat capacity for simplicity, we can see that this integrates to
These boxed equations relate state variables for adiabatic reversible changes of an ideal gas in a closed system.
Although not required, several rearrangements of this equation are useful for other problems. Note that we may insert the ideal gas law to convert to a formula relating T and P. Using V = RT/P,
Rearranging,
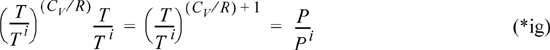
which becomes
We may also insert the ideal gas law into Eqn. 2.63 to convert to a formula relating P and V. Using T = PV/R,
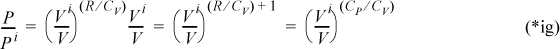
which may be written
The analysis of a piston+cylinder implied the assumption of a closed system. This might be a reasonable approximation for a single stroke of a combustion engine, but most chemical engineering applications involve continuous operation. Nevertheless, we can apply the lessons learned from the analysis of the closed system when extending to steady-state systems, as exemplified below.
Example 2.12. Continuous adiabatic, reversible compression of an ideal gas
Suppose 1 kmol/h of air at 5 bars and 298 K is adiabatically and reversibly compressed in a continuous process to 25 bars. What will be the outlet temperature and power requirement for the compressor in hp?
Solution
Note that air is composed primarily of oxygen and nitrogen and these both satisfy the stipulations for diatomic gases with their reduced temperatures high and their reduced pressures low. In other words, the ideal gas approximation with CP/R = 7/2 is clearly applicable. Next consider the energy balance. The system is the compressor. The system is open. Since it is a steady-state process with no heat transfer, the simplification of the energy balance has been discussed on page 73 and shown on page 72, and the energy balance becomes:
We can adapt Eqn. 2.31 for an ideal gas as follows:
dWS = dH = VdP
In this case, as we work down to step 4 in the strategy, we see that we cannot integrate the sides independently since P depends on T. Therefore, we need to combine terms before integrating.
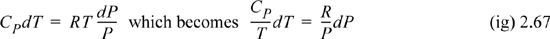
Once again, we have performed separation of variables. The rest of the derivation is entirely analogous to Example 2.11, and, in fact, the resultant formula is identical.
Steady-state adiabatic, reversible processing of an ideal gas results in the same relations as Example 2.11.
Note that this formula comes up quite often as an approximation for both open and closed systems. Making the appropriate substitutions,
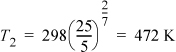
Adapting the adiabatic energy balance and assuming CPig = constant,
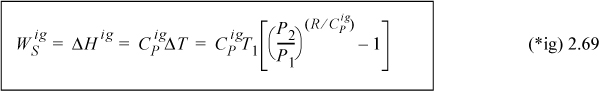
Steady-state adiabatic, reversible compression of an ideal gas.
Substituting, WS = 3.5·8.314·(472–298) = 5063 J/mole
At the given flow rate, and reiterating that this problem statement specifies a reversible process:
WSrev = 5063 J/mole·[1000mole/hr]·[1hr/3600sec]·[1hp/(745.7J/s)] = 1.9hp
We have systematically extended our analysis from a single step of a closed system, to a continuous system with no heat loss. Let’s consider isothermal operation.
Example 2.13. Continuous, isothermal, reversible compression of an ideal gas
Repeat the compression from the previous example, but consider steady-state isothermal compression. What will be the heat removal rate and power requirement for the compressor in hp?
Solution
Let’s return to the perspective of the section ‘Understanding Enthalpy and Shaft Work’ on page 54 and analyze the EC work and flow work for an ideal gas packet of unit mass. The WEC is,
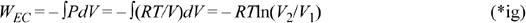
For an isothermal, ideal gas, V2/V1 = P1/P2. Noting the reciprocal and negative logarithm,
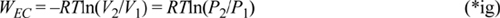
This is the work to isothermally squeeze an ideal gas packet of unit mass to a given pressure. The flow work performed on an ideal gas packet of unit mass is,
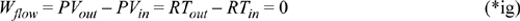
Therefore, the total requirement for isothermally compressing an ideal gas packet of unit mass is,
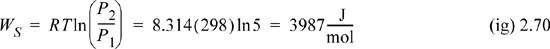
At the given flow rate, and reiterating that this problem statement specifies a reversible process,
WSrev = 3987 J/mole·[1000mole/hr]·[1hr/3600sec]·[1hp/745.7J/s] = 1.5 hp
Compared to adiabatic compression, the isothermal compressor requires less work. This happens because cooling withdraws energy from the system. It is difficult to achieve perfectly adiabatic or isothermal operation in practice, but adiabatic operation is usually a better approximation because compression is so rapid that there is insufficient time for heat transfer. Usually fluids are cooled after compression as we discuss in later chapters.
Here is a brain teaser. Suppose the process fluid had been steam instead of an ideal gas. How would you have solved the problem then? Note, for steam V ≠ RT/P and 
. We illustrate the answer in Example 4.16 on page 173.
Example 2.14. Heat loss from a turbine
High-pressure steam at a rate of 1100 kg/h initially at 3.5 MPa and 350°C is expanded in a turbine to obtain work. Two exit streams leave the turbine. Exiting stream (2) is at 1.5 MPa and 225°C and flows at 110 kg/h. Exiting stream (3) is at 0.79 MPa and is known to be a mixture of saturated vapor and liquid. A fraction of stream (3) is bled through a throttle valve to 0.10 MPa and is found to be 120°C. If the measured output of the turbine is 100 kW, estimate the heat loss of the turbine. Also, determine the quality of the steam in stream (3).
Solution
First draw a schematic. Designate boundaries. Both System A and System B are open steady-state systems.
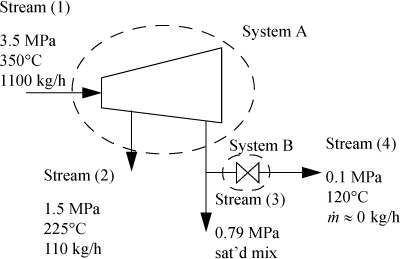
The mass balance gives 
. Next, determine which streams are completely specified: Streams (1), (2), and (4) are fully specified. Since Stream (3) is saturated, the temperature and pressure and specific enthalpies of the saturated vapor and liquid can be found, but the quality needs to be calculated to determine the overall molar enthalpy of the stream. From the steam tables we find H1 directly. For H2 we use linear interpolation. The value H(1.5 MPa, 225°C) is not available directly, so we need to first interpolate at 1.4 MPa between 200°C and 250°C to find H(1.4 MPa, 225°C) and then interpolate between this value and the value at 1.6 MPa:
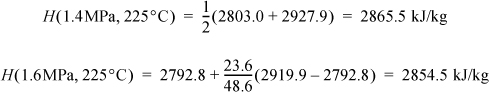
Then to find H2: H2 = 0.5·(2865.5 + 2854.5) = 2860.0 kJ/kg. For H4 we can interpolate in the superheated steam tables:
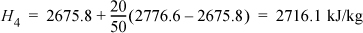
Recognize System B as a throttle valve; therefore, H3 = H4 = 2716.1 kJ/kg. We make a table to summarize the results so that we can easily find values:
The energy balance for System A gives, using 
given in the problem statement,
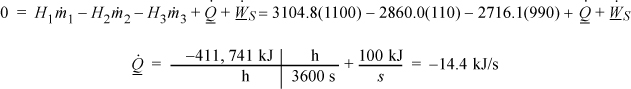
To find the quality of stream (3), 
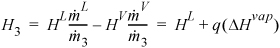
At 0.79 MPa from the sat’d P table, HL = 718.5 kJ/kg and ΔHV = 2049 kJ/kg.
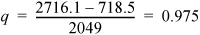
The energy balance for a non-adiabatic turbine is identical to the balance for an isothermal compressor, but the conclusions are entirely different. In the compressor, we want to minimize work, so the heat loss works to our advantage. For the turbine, we want to maximize work, so any loss of energy should be avoided.
The examples in this section comprise several important common scenarios, but they also illustrate a procedure for analyzing systems with systematically increasing sophistication. In the context of certain simplifying assumptions, like the ideal gas model, we can derive final working equations applicable to process calculations. When those assumptions are invalid, however, we can still apply the energy balance, but we are more careful in the generality of the results we obtain. Processes involving steam, for example, require something more than the ideal gas model, and additional tools are required to develop a general analysis.
Leave a Reply