Advanced Topics

Hints for Remembering the Auxiliary Relations

Auxiliary relations can be easily written by memorizing the fundamental relation for dU and the natural variables for the other properties. Note that {T,S} and {P,V} always appear in pairs, and each pair is a set of conjugate variables. A Legendre transformation performed on internal energy among conjugate variables changes the dependent variable and the sign of the term involving the conjugate variables. For example, to transform P and V, the product PV is added to U, resulting in Eqn. 6.5. To transform T and S, the product TS is subtracted: A = U – TS, dA = dU – TdS – SdT = –SdT – PdV. The pattern can be easily seen in the “Useful Derivatives” table on the front book end paper. Note that {T,S} always appear together, and {P,V} always appear together, and the sign changes upon transformation.

Jacobian Method of Derivative Manipulation

A partial derivative may be converted to derivatives of measurable properties with any two desired independent variables from the set {P,V,T}. Jacobian notation can be used to manipulate partial derivatives, and there are several useful rules for manipulating derivatives with the notation. The Joule-Thomson coefficient is a derivative that indicates how temperature changes upon pressure change at fixed enthalpy, , which is written in Jacobian notation as . Note how the constraint of constant enthalpy is incorporated into the notation. The rules for manipulation of the Jacobian notation are,

1. Jacobian notation represents a determinant of partial derivatives,

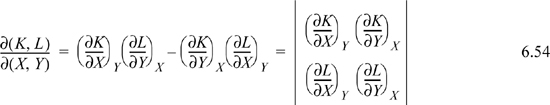
The Jacobian is particularly simple when the numerator and denominator have a common variable,

which is a special case of Eqn. 6.54.

2. When the order of variables in the numerator or denominator is switched, the sign of the Jacobian changes. Switching the order of variables in both the numerator and denominator results in no sign change due to cancellation. Consider switching the order of variables in the numerator,

3. The Jacobian may be inverted.

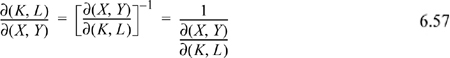
4. Additional variables may be interposed. When additional variables are interposed, it is usually convenient to invert one of the Jacobians.

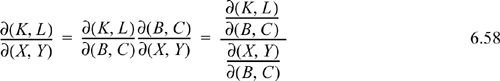
Manipulation of Derivatives

Before manipulating derivatives, the desired independent variables are selected. The selected independent variables will be held constant outside the derivatives in the final formula. The general procedure is to interpose the desired independent variables, rearrange as much as possible to obtain Jacobians with common variables in the numerator and denominator, write the determinant for any Jacobians without common variables; then use Maxwell relations, the expansion rule, and so on, to simplify the answer.

1. If the starting derivative already contains both the desired independent variables, the result of Jacobian manipulation is redundant with the triple product rule. The steps are: 1) write the Jacobian; 2) interpose the independent variables; 3) rearrange to convert to partial derivatives.

Example: Convert  to derivatives that use T and P as independent variables.

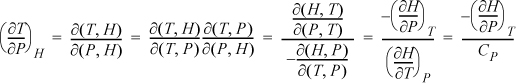
and the numerator can be simplified using the expansion rule as presented in Example 6.1.

2. If the starting derivative has just one of the desired independent variables, the steps are: 1) write the Jacobian; 2) interpose the desired variables; 3) write the determinant for the Jacobian without a common variable; 4) rearrange to convert to partial derivatives.

Example: Find a relation for the adiabatic compressibility,  in terms of derivatives using T, P as independent variables.

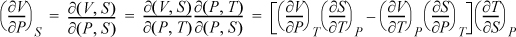
Now, including a Maxwell relation as we simplify the second term in square brackets, and then combining terms:

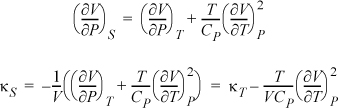
3. If the starting derivative has neither of the desired independent variables, the steps are: 1) write the Jacobian; 2) interpose the desired variables; 3) write the Jacobians as a quotient and write the determinants for both Jacobians; 4) rearrange to convert to partial derivatives.

Example: Find  in measurable properties using P and T as independent variables.

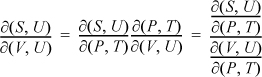
Writing the determinants for both Jacobians:

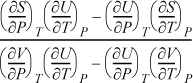
Now, using the expansion rule for the derivatives of U, and also introducing Maxwell relations,

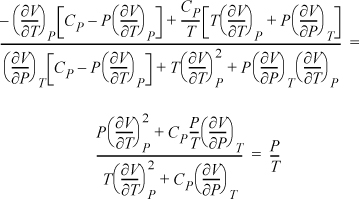
The result is particularly simple. We could have derived this directly if we had recognized that S and V are the natural variables for U. Therefore, dU = TdS – P dV = 0, . However, the exercise demonstrates the procedure and power of the Jacobian technique even though the result will usually not simplify to the extent of this example.