From the first law of thermodynamics for a closed reacting system we have���−���=��−��
where, ���



There is also no heat transfer because the process is defined to be adiabatic: ���=0



In the case of the constant pressure adiabatic flame temperature, the pressure of the system is held constant, which results in the following equation for the work:���=∫�����=�(��−��)
Again there is no heat transfer occurring because the process is defined to be adiabatic: ���=0
Recalling the definition of enthalpy we obtain ��=��

We see that the adiabatic flame temperature of the constant pressure process is lower than that of the constant volume process. This is because some of the energy released during combustion goes, as work, into changing the volume of the control system.
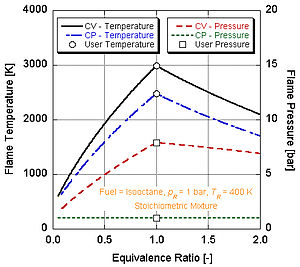
If we make the assumption that combustion goes to completion (i.e. forming only CO
2 and H
2O), we can calculate the adiabatic flame temperature by hand either at stoichiometric conditions or lean of stoichiometry (excess air). This is because there are enough variables and molar equations to balance the left and right hand sides,C�H�O�N�+(�O2+�N2)→�1CO2+�2H2O+�3N2+�4O2
Rich of stoichiometry there are not enough variables because combustion cannot go to completion with at least CO and H
2 needed for the molar balance (these are the most common products of incomplete combustion),C�H�O�N�+(�O2+�N2)→�1CO2+�2H2O+�3N2+�5CO+�6H2
However, if we include the water gas shift reaction,CO2+�2⇔CO+H2O
and use the equilibrium constant for this reaction, we will have enough variables to complete the calculation.
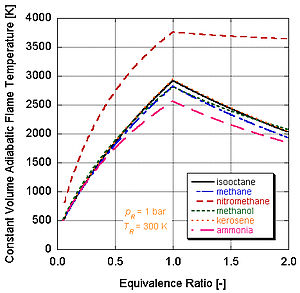
Different fuels with different levels of energy and molar constituents will have different adiabatic flame temperatures.
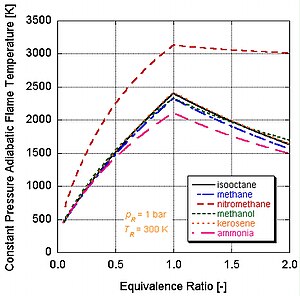
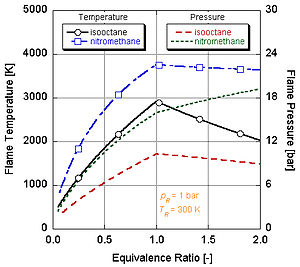
We can see by the following figure why nitromethane (CH3NO2) is often used as a power boost for cars. Since each molecule of nitromethane contains an oxidant with relatively high-energy bonds between nitrogen and oxygen, it can burn much hotter than hydrocarbons or oxygen-containing methanol. This is analogous to adding pure oxygen, which also raises the adiabatic flame temperature. This in turn allows it to build up more pressure during a constant volume process. The higher the pressure, the more force upon the piston creating more work and more power in the engine. It stays relatively hot rich of stoichiometry because it contains its own oxidant. However, continual running of an engine on nitromethane will eventually melt the piston and/or cylinder because of this higher temperature.

In real world applications, complete combustion does not typically occur. Chemistry dictates that dissociation and kinetics will change the composition of the products. There are a number of programs available that can calculate the adiabatic flame temperature taking into account dissociation through equilibrium constants (Stanjan, NASA CEA, AFTP). The following figure illustrates that the effects of dissociation tend to lower the adiabatic flame temperature. This result can be explained through Le Chatelier’s principle.







Leave a Reply