Computer modelling is a useful tool in representing and predicting atomic processes. A simulation has been created using IGOR Pro, a powerful graphing, data analysis, and programming tool for scientists and engineers produced by WaveMetrics. IGOR Pro is available for both Windows and Macintosh and a demo version can be downloaded from the WaveMetrics website. If you have access to a computer with IGOR Pro you can download the simulation, open it in IGOR Pro and experiment with it.
Download the simulation for use with IGOR Pro (260 KB)
If you do not have access to a computer with IGOR Pro, but have a high-speed connection to the Internet, you can run simulation movies generated by IGOR Pro for a limited number of parameter settings on the next page (but read this one first).
This simulation uses a 100×100 grid to represent a square 2-dimensional atomic array. This solid solution consists of two different types of atom: A and B. The A atoms can lie on two different types of site (alpha – yellow and beta – blue). The B atoms are black. The program demonstrates the expected action of the atomic system under the chosen input parameters.
The simulation uses a statistical approach (a Monte Carlo method, using random numbers to generate possible future outcome scenarios) to predict the atomic “jumps” within the solid solution, according to the interaction parameter and the temperature. By considering the change in free energy with mixing, the temperature and the interaction parameter determine whether one phase or two phases are most stable. The influence of the temperature on the equilibrium state can be seen in the solvus in the phase diagram.
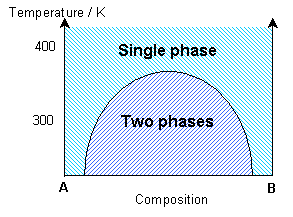
If the interaction parameter is positive, then A-A and B-B interactions will be energetically more favourable than A-B interactions. The positive enthalpy of mixing generates a tendency for the solution to form A-rich and B-rich regions (exsolution).
This phase separation produces A-rich and B-rich phases. At lower temperatures, more significant phase separation occurs. This gives larger regions of the two different phases, each of which are closer in composition to the end-members, A and B, due to the position of the solvus. Above the solvus temperature (which is around 375K for a composition of 50% A – 50% B), the solution remains fairly random, although some short range order can be seen, especially closer to the solvus, with preference for same bond types. At a lower composition of A (40% A – 60% B), the B regions are relatively larger.
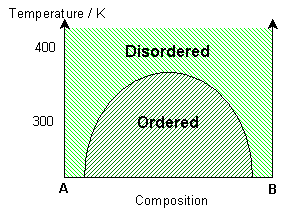
If the interaction parameter is negative, then A-B interactions will be energetically more favourable than A-A and B-B interactions. The negative enthalpy of mixing generates a tendency for the solution to form ordered compounds.
The ordered state of this system has a chessboard-like appearance, maximising the number of A-B bonds. By distinguishing the different types of A site (alpha – yellow and beta – blue), it is possible to see regions of different phase, i.e. ordered regions and anti-ordered regions. These anti-phase domains are separated by anti-phase boundaries.
At lower temperatures these domains are larger (less anti-phase boundaries). Just above the solvus, some short range ordering is seen, with preference for A-B bonds. At high temperatures, the solution remains random. With a higher percentage of B in the mixture, segregation of B along the anti-phase boundaries can be seen. More segregation is seen at lower temperatures.
If the solution is ideal, with all interactions energetically equivalent, then the interaction parameter and the enthalpy of mixing will be zero. A random solid solution is formed, with no preference for any of the bond types.
Leave a Reply