Demonstration

A mixture of equal quantities of cyclohexane and aniline contained in a sealed vial is heated to approximately 35 ºC (i.e. just above the critical temperature), using a water bath (or water from a hot tap). The mixture is allowed to cool, and a laser is pointed at the vial so that it shines onto a screen opposite, as shown in the diagram below.

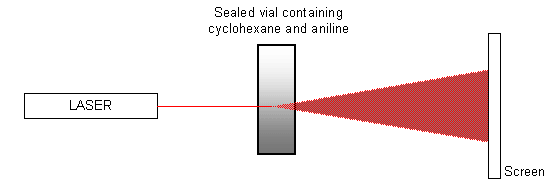
When the critical temperature is reached and the mixture goes from a single phase to two phases, the spot of light on the screen is disrupted as the phases separate. The spot ‘flickers’ and then becomes totally diffuse. It will eventually form a single spot again once the transition is completed and the two chemicals have completely separated. The pattern of events can also be seen in reverse as the mixture is heated.

Video showing the laser light (as seen on the screen) flickering and spreading out to become
completely opaque as the mixture cools through the transition temperature

The video has been speeded up by a factor of about 10.

Video showing the vial, which has been filmed perpendicular to the direction of the laser light (left to right)

Initially, the laser light is seen as a single beam passing through the mixture, but as the transition point is reached, the beam spreads out. The single beam eventually reforms, once the transition is complete. This video has been speeded up by a factor of about 200.

Precipitates from solid solution

The precipitation of a solid phase from a liquid matrix is governed by a balance between the thermodynamic driving force and the energy penalty for creating new solid-liquid surface interfaces. This determines the size and shape of the precipitates. The precipitation of a solid phase from a solid parent phase is very similar.

There are various types of interface between solid phases:

Coherent – there is perfect registry of the lattices.
Coherent with strain – it is quite likely for there to be some strain with the interface, due to imperfect matching. The strain energy increases with the size of the growing particle, and there is a transition to a semi-coherent interface.
Semi-coherent interface – the introduction of dislocations reduces the strain energy (but they themselves contribute to the energy of the system).
Incoherent – there is no matching of the interface.

Diagram of coherent with strain interface

In general, the interfacial free energy will be minimised with better matching of the two phases. Incoherent interfaces have high energy and are relatively mobile because of the greater freedom of atomic motion.

The stresses present in the parent matrix as the precipitate grows strongly influences the shape of the precipitate. By modelling the precipitate as an ellipsoid of revolution, the following graph shows how the strain energy is related to the shape.

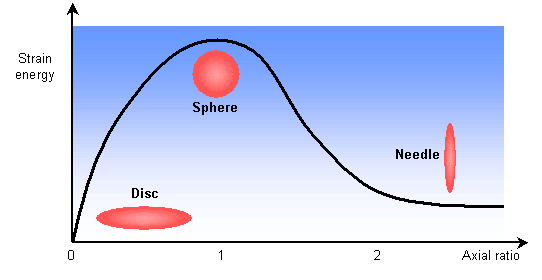
Graph of strain energy against axial ratio

Growth as discs or plates is clearly preferred. A precipitate particle will likely have some coherent and some incoherent interfaces with the matrix. The greater mobility of the incoherent interfaces leads to faster growth in these directions. This anisotropic growth leads to plate and disc morphologies. The bounding coherent interfaces will be parallel to crystallographic planes in the matrix.

Solid solution precipitation/exsolution is used to strengthen many alloys. This is known as precipitation hardening, or age hardening. It involves quenching an alloy to a supersaturated state (where the amount of dissolved solute is greater than the equilibrium amount predicted by the phase diagram). A heating schedule can then be applied to control the nature of the precipitation. For example in Al-Cu, a very fine dispersion of θ particles hardens the α phase. This age-hardened alloy is used in aerospace applications.

View micrograph of a precipitation hardened sample of Al-Cu

At lower temperatures, it is preferable to have incoherent precipitates, as the greater strains produce more resistance on dislocation motion. At higher temperatures however, the greater mobililty of the incoherent interfaces allows larger particles to grow at the expense of smaller ones (called coarsening), and the system becomes less effective at strengthening. So for high temperature use, coherent particles are used, such as the γ’ precipitate in nickel-based superalloys (here a phenomenon called order hardening provides the strengthening mechanism, rather than the strain fields).

View micrograph of an order hardened sample of Nickel superalloy

Ceramics, which are typically brittle, can also benefit from solid solution precipitation. Zirconia based compounds can be toughened by having tetragonal structure particles in the monoclinic matrix. Propagation of cracks through the zirconia requires the transformation of these precipitates to the monoclinic form. This requires an input of energy, provided by the stress, hence the material is toughened.

Another use of solid solution precipitation lies in nano-materials. By precipitating from a solid solution, the nanometre (10^-9m) scale of the microstructure can provide many beneficial effects. For example, the presence of 5 nm diameter carbide particles in steel piano wires helps make it the world’s strongest structural material (with some ductility). Precipitation from a liquid phase is too fast to produce such small scale particles.

Monte Carlo simulation

Computer modelling is a useful tool in representing and predicting atomic processes. A simulation has been created using IGOR Pro, a powerful graphing, data analysis, and programming tool for scientists and engineers produced by WaveMetrics. IGOR Pro is available for both Windows and Macintosh and a demo version can be downloaded from the WaveMetrics website. If you have access to a computer with IGOR Pro you can download the simulation, open it in IGOR Pro and experiment with it.

Download the simulation for use with IGOR Pro (260 KB)

If you do not have access to a computer with IGOR Pro, but have a high-speed connection to the Internet, you can run simulation movies generated by IGOR Pro for a limited number of parameter settings on the next page (but read this one first).

This simulation uses a 100×100 grid to represent a square 2-dimensional atomic array. This solid solution consists of two different types of atom: A and B. The A atoms can lie on two different types of site (alpha – yellow and beta – blue). The B atoms are black. The program demonstrates the expected action of the atomic system under the chosen input parameters.

The simulation uses a statistical approach (a Monte Carlo method, using random numbers to generate possible future outcome scenarios) to predict the atomic “jumps” within the solid solution, according to the interaction parameter and the temperature. By considering the change in free energy with mixing, the temperature and the interaction parameter determine whether one phase or two phases are most stable. The influence of the temperature on the equilibrium state can be seen in the solvus in the phase diagram.

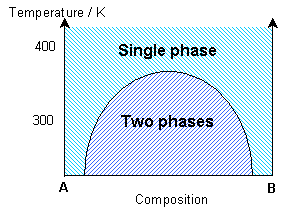
If the interaction parameter is positive, then A-A and B-B interactions will be energetically more favourable than A-B interactions. The positive enthalpy of mixing generates a tendency for the solution to form A-rich and B-rich regions (exsolution).

This phase separation produces A-rich and B-rich phases. At lower temperatures, more significant phase separation occurs. This gives larger regions of the two different phases, each of which are closer in composition to the end-members, A and B, due to the position of the solvus. Above the solvus temperature (which is around 375K for a composition of 50% A – 50% B), the solution remains fairly random, although some short range order can be seen, especially closer to the solvus, with preference for same bond types. At a lower composition of A (40% A – 60% B), the B regions are relatively larger.

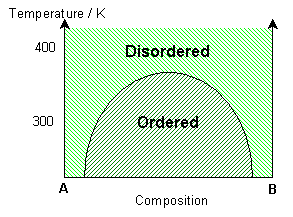
If the interaction parameter is negative, then A-B interactions will be energetically more favourable than A-A and B-B interactions. The negative enthalpy of mixing generates a tendency for the solution to form ordered compounds.

The ordered state of this system has a chessboard-like appearance, maximising the number of A-B bonds. By distinguishing the different types of A site (alpha – yellow and beta – blue), it is possible to see regions of different phase, i.e. ordered regions and anti-ordered regions. These anti-phase domains are separated by anti-phase boundaries.

At lower temperatures these domains are larger (less anti-phase boundaries). Just above the solvus, some short range ordering is seen, with preference for A-B bonds. At high temperatures, the solution remains random. With a higher percentage of B in the mixture, segregation of B along the anti-phase boundaries can be seen. More segregation is seen at lower temperatures.

If the solution is ideal, with all interactions energetically equivalent, then the interaction parameter and the enthalpy of mixing will be zero. A random solid solution is formed, with no preference for any of the bond types.

Web version of Monte Carlo simulation

This page provides a limited web-based version of the Monte Carlo simulation in case you are not able to run it in IGOR Pro. There are a limited number of choices of interaction parameter, temperature and composition. Video clips generated by running the simulation in IGOR Pro show the progression from an initially disordered state to the state determined by the input parameters. The video clip files are 2 to 3 MB in size, so if you are on a slow Internet connection you may prefer to view an image of the final state reached instead.

As described on the previous page, the A atoms can lie on two different types of site (alpha – yellow and beta – blue), while the B atoms are black.

Summary

Solid solutions consist of a mixture of components that are completely miscible with one another, and hence are a single solid phase. This Teaching and Learning Package has discussed the concept of solid solutions in two-component systems. By taking an atomistic approach, the processes of exsolution and ordering can be described and even modelled (using a Monte Carlo simulation). The interaction parameter, a quantitative representation of the tendency for bonding in the mixture, has been shown to be a critical factor in determining the equilibrium state of the mixture. In other words, the miscibility of one component with the other is dependent on the underlying thermodynamics.

Relating this TLP to the Phase Diagrams and Solidification TLP, the presence of solid solutions in phase diagrams has been discussed. Achieving a solid solution has been seen to be advantageous in terms of strengthening and hardening (via precipitates). The scale of the precipitates possible from a supersaturated solid solution can be significantly smaller than that possible with solidification from a liquid.

Owing to the difficulty in demonstrating phase separation in solids, a demonstration involving a mixture of cyclohexane and aniline (both in liquid form) has been used instead. The ability of this system to scatter light during the change between one and two phases allows the transition to be easily identified.

Questions

Which of the regions of this Fe-C phase diagram are solid solutions?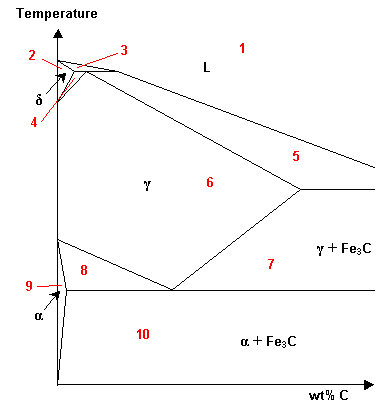a1, 2, 6, 9b2, 6, 7, 8, 9, 10c2, 6, 9d2, 4, 6, 8, 9e4, 7, 8, 10f7, 10g1, 2, 6, 7, 9, 10
Will the following factors affect the extent of solid solubility?YesNoaCompositionYesNobTemperatureYesNocAtomic radiiYesNodCrystallographic structureYesNoeElectronegativityYesNofValencyYesNogInteraction parameter
How might a supersaturated solid solution be formed, using the following phase diagram? α and β are solid solutions.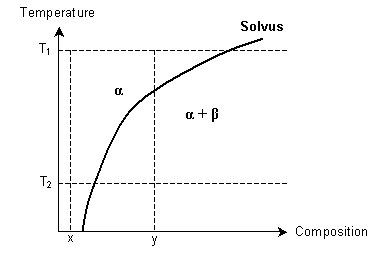aQuench from T₁ to T₂ with composition xbCool slowly from T₁ to T₂ with composition xcQuench from T₁ to T₂ with composition ydCool slowly from T₁ to T₂ with composition y
Which of these will not explain the strengthening of a solid solution?aLattice distortionbOrder hardeningcStress fieldsdInteraction with dislocations
Which of these is not a feature of exsolution in a solid solution?aNegative interaction parameterbPositive enthalpy of mixingcFormation of A rich and B rich regionsdIncrease in short range order

Going further

Books

A. Putnis, Introduction to Mineral Sciences, CUP 1992

Websites

Phase Diagrams of Alloys
A collection of phase diagrams, previously hosted by the Georgia Institute of Technology
Teach Yourself Phase Diagrams
A Flash interactive tutorial on phase diagrams based in the Department of Engineering at the University of Cambridge.

Exsolution and cation ordering

Polymer mixtures

Mixtures of two polymers (polymer blends) also show transitions between single phase and two-phase states. If the enthalpic interactions are unfavourable, the mixture will exhibit an upper critical solution temperature. Thus the polymers will be immiscible at lower temperatures. They will be miscible at high temperatures due to reduced enthalpic interactions.

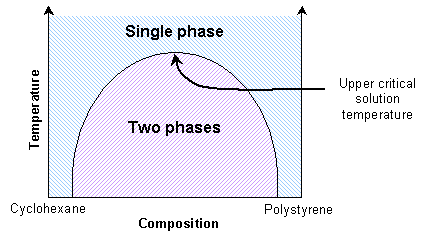
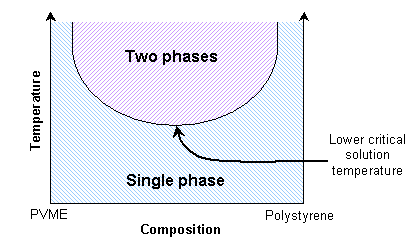
This is similar to the solid solutions previously mentioned. Some polymer blends can exhibit a lower critical solution temperature instead. A mixture of polystyrene and poly(vinyl methylene) is miscible at lower temperatures due to favourable enthalpic interactions, and immiscible at higher temperatures due to free volume differences.

Academic consultants: Zoe Barber and Richard Harrison (University of Cambridge)
Content development: Chris Shortall and Jessica Gwynne
Photography and video: Brian Barber and Carol Best
Web development: Dave Hudson

This TLP was prepared when DoITPoMS was funded by the Higher Education Funding Council for England (HEFCE) and the Department for Employment and Learning (DEL) under the Fund for the Development of Teaching and Learning (FDTL).

2004-2024 University of Cambridge.
Except where otherwise noted, content is licensed under a
Creative Commons Attribution – NonCommercial-ShareAlike 4.0 International.

Department of Materials Science & Metallurgy/Privacy & Cookies/About DoITPoMS